题目内容
4.在Rt△ABC中,∠C=90°,AB=15,AC:BC=3:4,则这个直角三角形的面积是( )| A. | 24 | B. | 48 | C. | 54 | D. | 108 |
分析 设AC=3x,则BC=4x,然后根据勾股定理得到AC2+BC2=AB2,求出x2的值,继而根据三角形的面积公式求出答案.
解答 解:设AC=3x,则BC=4x,
根据勾股定理有AC2+BC2=AB2,
即(3x)2+(4x)2=152,得:x2=9,
则△ABC的面积=$\frac{1}{2}$×3x×4x=6x2=54.
故选:C.
点评 本题考查勾股定理的知识,难度适中,关键是根据勾股定理公式求出x2的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.对于函数y=-$\frac{3}{x}$,当x<0时,函数图象位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.下列运算中错误的是( )
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | $\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ | C. | 2 $\sqrt{2}$+3$\sqrt{2}$=5$\sqrt{2}$ | D. | $\sqrt{(\sqrt{2}-\sqrt{3})^{2}}$=$\sqrt{2}-\sqrt{3}$ |
14.观察下表,按你发现的规律填空
已知$\sqrt{15}$=3.873,则$\sqrt{150000}$的值为387.3.
| a | 0.0121 | 1.21 | 121 | 12100 |
| $\sqrt{a}$ | 0.11 | 1.1 | 11 | 110 |
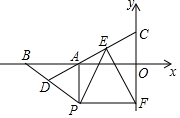 已知:如图,平面直角坐标系中,点B坐标为(-4,0),点A为线段OB中点,点P在第三象限,且AP⊥y轴,PF⊥y轴,D为BP中点,连接DA并延长交y轴于点C,FE⊥DC.
已知:如图,平面直角坐标系中,点B坐标为(-4,0),点A为线段OB中点,点P在第三象限,且AP⊥y轴,PF⊥y轴,D为BP中点,连接DA并延长交y轴于点C,FE⊥DC.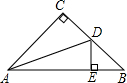 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB交AB于点E,AB=4$\sqrt{2}$cm,求△BDE的周长.
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB交AB于点E,AB=4$\sqrt{2}$cm,求△BDE的周长.