题目内容
15.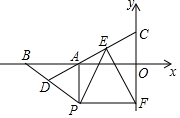 已知:如图,平面直角坐标系中,点B坐标为(-4,0),点A为线段OB中点,点P在第三象限,且AP⊥y轴,PF⊥y轴,D为BP中点,连接DA并延长交y轴于点C,FE⊥DC.
已知:如图,平面直角坐标系中,点B坐标为(-4,0),点A为线段OB中点,点P在第三象限,且AP⊥y轴,PF⊥y轴,D为BP中点,连接DA并延长交y轴于点C,FE⊥DC.(1)直接写出点A坐标(-2,0);
(2)求证:BP=AC;
(3)若点E为AC中点,连接PE,判断△PEF的形状,并说明理由.
分析 (1)根据点B的坐标以及中点的定义即可解决问题.
(2)只要证明△PBA≌△CAO即可.
(3)如图延长PE交y轴于M.由△PAE≌△MCE,推出EP=EM,由∠PFM=90°,推出EF=PE(直角三角形的斜边上的中线等于斜边的一半).
解答 (1)解:∵B(-4,0),AB=OA,
∴点A坐标为(-2,0).
故答案为(-2,0)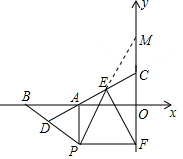
(2)证明:∵PA⊥AB,
∴∠BAP=∠AOC=90°,
∵BD=DP,
∴AD=DB=PD,
∴∠ABP=∠BDA=∠CAO,
在△PBA和△CAO中,
$\left\{\begin{array}{l}{∠PAB=∠AOC}\\{AB=AO}\\{∠ABP=∠CAO}\end{array}\right.$,
∴△PBA≌△CAO,
∴PB=CA.
(3)解:结论:△PEF是等腰三角形.
理由:如图延长PE交y轴于M.
∵PA∥CM,
∴∠PAE=∠MCE,
在△PAE和△MCE中,
$\left\{\begin{array}{l}{∠PAE=∠MCE}\\{AE=EC}\\{∠AEP=∠CEM}\end{array}\right.$,
∴△PAE≌△MCE,
∴EP=EM,
∵∠PFM=90°,
∴EF=PE(直角三角形的斜边上的中线等于斜边的一半).
∴△PEF是等腰三角形.
点评 本题考查三角形综合题、全等三角形的判定和性质、直角三角形斜边中线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.在Rt△ABC中,∠C=90°,AB=15,AC:BC=3:4,则这个直角三角形的面积是( )
| A. | 24 | B. | 48 | C. | 54 | D. | 108 |
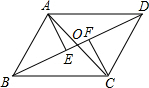 已知:如图,AB=CD,AE⊥BD于E,CF⊥BD于F,AE=CF.
已知:如图,AB=CD,AE⊥BD于E,CF⊥BD于F,AE=CF.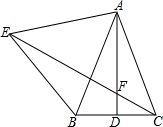 如图,△ABC中,AB=AC,AD是BC边上的中线,以AB为边向外作等边△ABE,与直线AD交于点F.
如图,△ABC中,AB=AC,AD是BC边上的中线,以AB为边向外作等边△ABE,与直线AD交于点F. 二次函数y=$\frac{2}{3}$x2的函数图象如图,点A0位于坐标原点,点A1,A2,A3…A10 在y轴的正半轴上,点B1,B2,B3…B10在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都为等边三角形,则△A9B10A10的边长为10.
二次函数y=$\frac{2}{3}$x2的函数图象如图,点A0位于坐标原点,点A1,A2,A3…A10 在y轴的正半轴上,点B1,B2,B3…B10在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都为等边三角形,则△A9B10A10的边长为10.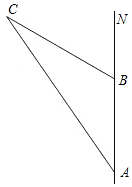 某轮船上午8时从A岛出发,以20海里/小时的速度向正北方向航行,如图,上午10时到达B岛,此时得到消息,在C岛周围15海里内有暗礁,经测量得∠NAC=15°,∠NBC=30°,问该轮船继续向北航行有无触礁危险?
某轮船上午8时从A岛出发,以20海里/小时的速度向正北方向航行,如图,上午10时到达B岛,此时得到消息,在C岛周围15海里内有暗礁,经测量得∠NAC=15°,∠NBC=30°,问该轮船继续向北航行有无触礁危险?