题目内容
12.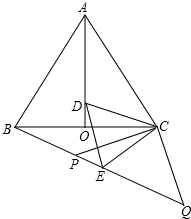 如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.(1)求证:∠ACD=∠BCE;
(2)求证:△ACD≌△BCE;
(3)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长.
分析 (1)由△ABC与△DCE是等边三角形,可得AC=BC,DC=EC,∠ACB=∠DCE=60°,又由∠ACD+∠DCB=∠ECB+∠DCB=60°,即可证得∠ACD=∠BCE
(2)根据SAS即可证得△ACD≌△BCE;
(3)首先过点C作CH⊥BQ于H,由等边三角形的性质,即可求得∠DAC=30°,则根据等腰三角形与直角三角形中的勾股定理即可求得PQ的长.
解答 (1)证明:∵△ABC与△DCE是等边三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠ECB+∠DCB=60°,
∴∠ACD=∠BCE;
(2)证明:在△ACD和△BCE中,
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=EC}\end{array}\right.$
∴△ACD≌△BCE(SAS);
(2)解:过点C作CH⊥BQ于H,
∵△ABC是等边三角形,AO是角平分线,
∴∠DAC=30°,
∵△ACD≌△BCE,
∴∠PBC=∠DAC=30°,
∴在Rt△BHC中,CH=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4,
∵PC=CQ=5,CH=4,
∴PH=QH=3,
∴PQ=6.
点评 此题考查了全等三角形的判定与性质,等腰三角形、等边三角形以及直角三角形的性质等知识.综合性较强,解题时要注意数形结合思想的应用.

练习册系列答案
相关题目
3.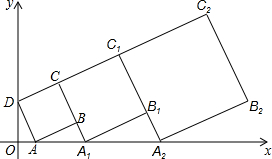 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )| A. | 5($\frac{3}{2}$)2010 | B. | 5($\frac{9}{4}$)2010 | C. | 5($\frac{9}{4}$)2011 | D. | 5($\frac{3}{2}$)2011 |
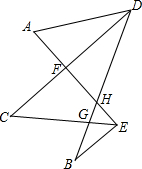 如图,∠A=60°,∠B=30°,CD,CE分别平分∠ADB和∠AEB,求∠C的度数.
如图,∠A=60°,∠B=30°,CD,CE分别平分∠ADB和∠AEB,求∠C的度数.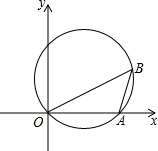 如图,已知点A(8,0),sin∠AB0=$\frac{4}{5}$,抛物线经过点0、A,且顶点在△A0B的外接圆上,则此抛物线的表达式为y=-$\frac{1}{2}$x2+4x.
如图,已知点A(8,0),sin∠AB0=$\frac{4}{5}$,抛物线经过点0、A,且顶点在△A0B的外接圆上,则此抛物线的表达式为y=-$\frac{1}{2}$x2+4x.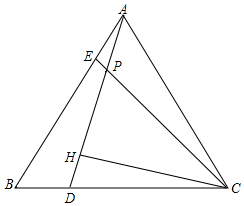 如图,△ABC是等边三角形,D、E分别在BC、AB上,且AE=BD,连接AD、CE交于P,过点C作CH⊥AD于H.
如图,△ABC是等边三角形,D、E分别在BC、AB上,且AE=BD,连接AD、CE交于P,过点C作CH⊥AD于H.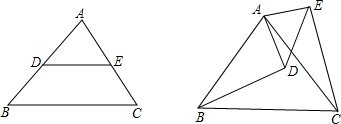
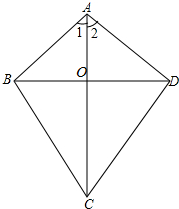 在四边形ABCD中,AC与BD相交于点D,AB=AD,BC=DC,
在四边形ABCD中,AC与BD相交于点D,AB=AD,BC=DC,