题目内容
11.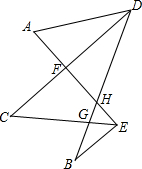 如图,∠A=60°,∠B=30°,CD,CE分别平分∠ADB和∠AEB,求∠C的度数.
如图,∠A=60°,∠B=30°,CD,CE分别平分∠ADB和∠AEB,求∠C的度数.
分析 由三角形的内角和在△AHD和△BHE可知:∠A+∠ADB=∠B+∠AEB,推出∠AEB=30°+∠ADB,再由∠CFE=180°-∠A-∠ADF,在△CEF中,利用三角形的内角和以及CD,CE分别平分∠ADB和∠AEB,整理得出∠C的度数即可.
解答 解:∵在△AHD和△BHE中,∠A=60°,∠B=30°,
∴∠A+∠ADB=∠B+∠AEB,
∴∠AEB=30°+∠ADB,
∵CE分别平分∠ADB和∠AEB,
∴∠ADF=$\frac{1}{2}$∠ADB,∠CEA=$\frac{1}{2}$∠AEB,
又∵∠CFE=180°-∠A-∠ADF=120°-$\frac{1}{2}$∠ADB,
∴∠C=180°-∠CFE-∠FEC
=180°-(120°-$\frac{1}{2}$∠ADB)-$\frac{1}{2}$∠AEB
=60°+$\frac{1}{2}$∠ADB-$\frac{1}{2}$(30°+∠ADB)
=45°.
点评 此题考查三角形的内角和定理,三角形外角的性质,角平分线的意义,掌握三角形的内角和180°是解决问题的关键.

练习册系列答案
相关题目
1.将抛物线y=2x2+2向右平移1个单位后所得抛物线的解析式是( )
| A. | y=2x2+3 | B. | y=2x2+1 | C. | y=2(x+1)2+2 | D. | y=2(x-1)2+2 |
3.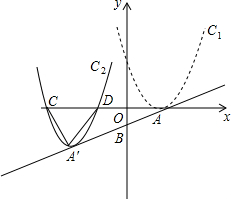 如图,抛物线C1:y=(x-2)2的顶点为A,直线AB:y=$\frac{1}{2}$x-1与y轴交于B点.将抛物线C1沿AB方向平移得到抛物线C2,顶点为A′,C2于x轴交于C、D两点,若△A′CD为正三角形,则AA′的长是( )
如图,抛物线C1:y=(x-2)2的顶点为A,直线AB:y=$\frac{1}{2}$x-1与y轴交于B点.将抛物线C1沿AB方向平移得到抛物线C2,顶点为A′,C2于x轴交于C、D两点,若△A′CD为正三角形,则AA′的长是( )
 如图,抛物线C1:y=(x-2)2的顶点为A,直线AB:y=$\frac{1}{2}$x-1与y轴交于B点.将抛物线C1沿AB方向平移得到抛物线C2,顶点为A′,C2于x轴交于C、D两点,若△A′CD为正三角形,则AA′的长是( )
如图,抛物线C1:y=(x-2)2的顶点为A,直线AB:y=$\frac{1}{2}$x-1与y轴交于B点.将抛物线C1沿AB方向平移得到抛物线C2,顶点为A′,C2于x轴交于C、D两点,若△A′CD为正三角形,则AA′的长是( )| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
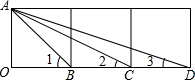 如图,由三个小正方形拼成的矩形,给出下列结论:
如图,由三个小正方形拼成的矩形,给出下列结论: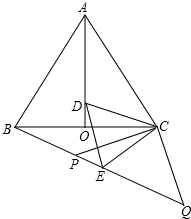 如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.