题目内容
20.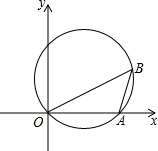 如图,已知点A(8,0),sin∠AB0=$\frac{4}{5}$,抛物线经过点0、A,且顶点在△A0B的外接圆上,则此抛物线的表达式为y=-$\frac{1}{2}$x2+4x.
如图,已知点A(8,0),sin∠AB0=$\frac{4}{5}$,抛物线经过点0、A,且顶点在△A0B的外接圆上,则此抛物线的表达式为y=-$\frac{1}{2}$x2+4x.
分析 根据圆周角定理以及勾股定理和垂径定理得出E,F点的坐标,进而利用顶点式求出抛物线解析式即可.
解答 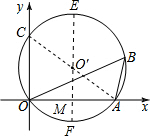 解:如图所示:连接AC,过圆心O′作EF⊥OA,
解:如图所示:连接AC,过圆心O′作EF⊥OA,
∵∠AOC=90°,∠ABO=∠OCA,
∴$\frac{AO}{AC}$=$\frac{4}{5}$,
∵点A(8,0),
∴AC=10,
根据题意得出:AM=OM=4,AO′=5,
∴MO′=3,∴MF=2,
∴F点坐标为:(4,-2),
设过O,A,F的抛物线解析式为:y=a(x-4)2-2,
将A代入(8,0)得:0=a(8-4)2-2,
解得:a=$\frac{1}{8}$,
∴此时抛物线解析式为:y=$\frac{1}{8}$(x-4)2-2=$\frac{1}{8}$x2-x,
根据题意得出:AM=OM=4,AO′=5,
∴MO′=3,∴ME=8,
∴E点坐标为:(4,8),
设过O,A,E的抛物线解析式为:y=a(x-4)2+8,
将A代入(8,0)得:
0=a(8-4)2+8,
解得:a=-$\frac{1}{2}$,
∴此时抛物线解析式为:y=-$\frac{1}{2}$(x-4)2+8=-$\frac{1}{2}$x2+4x,
故答案是:y=-$\frac{1}{2}$x2+4x.
点评 此题主要考查了利用顶点式求抛物线解析式以及垂径定理、圆周角定理、勾股定理的应用,根据已知得出E,F点坐标是解题关键.

练习册系列答案
相关题目
11.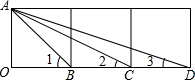 如图,由三个小正方形拼成的矩形,给出下列结论:
如图,由三个小正方形拼成的矩形,给出下列结论:
①△ABC∽△ACD;②△BAC∽△BDA;③∠1=∠2+∠3;④∠1+∠2+∠3=90°.其中一定成立的个数为( )
 如图,由三个小正方形拼成的矩形,给出下列结论:
如图,由三个小正方形拼成的矩形,给出下列结论:①△ABC∽△ACD;②△BAC∽△BDA;③∠1=∠2+∠3;④∠1+∠2+∠3=90°.其中一定成立的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.扬州瘦西湖隧道是全国唯一一个在“AAAA”景区底下开凿的交通隧道,也打破了扬州没有隧道的历史,为了保护隧道的安全,晴天和雨天通过隧道的车速最高分别为60千米/小时和50千米/小时,那么晴天和雨天以最高车速通过隧道的平均速度是( )千米/小时.
| A. | 50 | B. | $\frac{600}{11}$ | C. | 55 | D. | 60 |
15.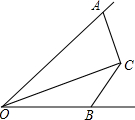 如图,在∠AOB中,OC平分∠AOB,OA>OB,∠OAC+∠OBC=180°,则AC与BC之间的大小关系是( )
如图,在∠AOB中,OC平分∠AOB,OA>OB,∠OAC+∠OBC=180°,则AC与BC之间的大小关系是( )
 如图,在∠AOB中,OC平分∠AOB,OA>OB,∠OAC+∠OBC=180°,则AC与BC之间的大小关系是( )
如图,在∠AOB中,OC平分∠AOB,OA>OB,∠OAC+∠OBC=180°,则AC与BC之间的大小关系是( )| A. | AC=BC | B. | AC>BC | C. | AC<BC | D. | 无法确定 |
5.已知$\frac{b}{a}$=$\frac{2}{3}$,则$\frac{a}{a+b}$的值是( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
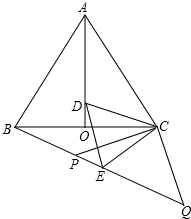 如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.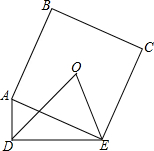 如图,在Rt△ADE中,∠ADE=90°,AD=3cm,DE=5cm,以AE为边向外作正方形ABCE,O为正方形ABCE的中心,则△DOE的面积为10cm2.
如图,在Rt△ADE中,∠ADE=90°,AD=3cm,DE=5cm,以AE为边向外作正方形ABCE,O为正方形ABCE的中心,则△DOE的面积为10cm2.