题目内容
在平面直角坐标系中的△ABC,AB=BC=5,点A坐标为(0,4),点B坐标为(-3,0).
(1)若点C在坐标轴上,则点C的坐标是 ;
(2)如图1,当∠ABC=90°时,则点C的坐标是 ;
(3)如图2,当∠ABC=60°,BC边与y轴交于点D,点E为AC边上一点,且AE=CD,连接BE与y轴交于点P,求证:PB=2PO.

(1)若点C在坐标轴上,则点C的坐标是
(2)如图1,当∠ABC=90°时,则点C的坐标是
(3)如图2,当∠ABC=60°,BC边与y轴交于点D,点E为AC边上一点,且AE=CD,连接BE与y轴交于点P,求证:PB=2PO.

考点:全等三角形的判定与性质,坐标与图形性质,含30度角的直角三角形
专题:
分析:(1))由AB=BC=5,A(0,4),B(-3,0),容易得出点C坐标有三个解;
(2)作CD⊥x轴于点D,证明△BCD≌△ABO,得出BD=AO=4,CD=BO=3,OD=1,从而得出点C坐标是 (1,-3);
(3)先证明△ABE≌CAD(SAS),得出∠ABE=∠CAD,证出∠BPO=60°,∠OBP=30°,即可证出PB=2PO.
(2)作CD⊥x轴于点D,证明△BCD≌△ABO,得出BD=AO=4,CD=BO=3,OD=1,从而得出点C坐标是 (1,-3);
(3)先证明△ABE≌CAD(SAS),得出∠ABE=∠CAD,证出∠BPO=60°,∠OBP=30°,即可证出PB=2PO.
解答:解:(1)∵AB=BC=5,A(0,4),B(-3,0),点C在坐标轴上,
∴点C坐标是 (0,-4)或(-8,0)或(2,0);
故答案为:(0,-4)或(-8,0)或(2,0);
(2)作CD⊥x轴于点D,如图1所示:
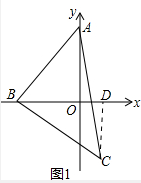 则∠CDB=∠AOB=∠ABC=90°,
则∠CDB=∠AOB=∠ABC=90°,
∴∠BCD+∠CBD=90°,∠ABO+∠CBD=90°,
∴∠BCD=∠ABO,
在△BCD和△ABO中,
∴△BCD≌△ABO(AAS),
∴BD=AO=4,CD=BO=3,
∴OD=4-3=1,
点C坐标是 (1,-3);
故答案为:(1,-3);
(3)证明:∵AB=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=∠C=∠ABC=60°,AB=AC,
在△ABE和△CAD中,
∴△ABE≌CAD(SAS),
∴∠ABE=∠CAD,
∴∠BPO=∠ABP+∠BAP=∠CAD+∠BAP=∠BAC=60°,
∴∠OBP=90°-60°=30°,
∵AO⊥BO,
∴PB=2PO.
∴点C坐标是 (0,-4)或(-8,0)或(2,0);
故答案为:(0,-4)或(-8,0)或(2,0);
(2)作CD⊥x轴于点D,如图1所示:
 则∠CDB=∠AOB=∠ABC=90°,
则∠CDB=∠AOB=∠ABC=90°,∴∠BCD+∠CBD=90°,∠ABO+∠CBD=90°,
∴∠BCD=∠ABO,
在△BCD和△ABO中,
|
∴△BCD≌△ABO(AAS),
∴BD=AO=4,CD=BO=3,
∴OD=4-3=1,
点C坐标是 (1,-3);
故答案为:(1,-3);
(3)证明:∵AB=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=∠C=∠ABC=60°,AB=AC,
在△ABE和△CAD中,
|
∴△ABE≌CAD(SAS),
∴∠ABE=∠CAD,
∴∠BPO=∠ABP+∠BAP=∠CAD+∠BAP=∠BAC=60°,
∴∠OBP=90°-60°=30°,
∵AO⊥BO,
∴PB=2PO.
点评:本题考查了坐标与图形性质、全等三角形的判定与性质以及含30°的直角三角形的性质;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
 如图,在?ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,当点E,F满足下列条件时,四边形DEBF不一定是平行四边形( )
如图,在?ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,当点E,F满足下列条件时,四边形DEBF不一定是平行四边形( )| A、AE=CF |
| B、DE=BF |
| C、∠ADE=∠CBF |
| D、∠AED=∠CFB |
已知半径为3的圆⊙O外有一条直线,已知⊙O与直线相切,则圆心到上一点的最短距离为( )
| A、1 | B、2 | C、3 | D、4 |
 如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,求∠MON.
如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,求∠MON. 如图,点A,B,C,D在同一个圆上,且B是弧AC的中点,则图中相等的圆周角有几对?
如图,点A,B,C,D在同一个圆上,且B是弧AC的中点,则图中相等的圆周角有几对? 如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E,F分别在BC,AB边上且F(1,4).
如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E,F分别在BC,AB边上且F(1,4). 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,交y轴于点C,且A(-3,0),C(0,-3),对称轴为直线x=-1.
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,交y轴于点C,且A(-3,0),C(0,-3),对称轴为直线x=-1.