题目内容
 如图,在?ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,当点E,F满足下列条件时,四边形DEBF不一定是平行四边形( )
如图,在?ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,当点E,F满足下列条件时,四边形DEBF不一定是平行四边形( )| A、AE=CF |
| B、DE=BF |
| C、∠ADE=∠CBF |
| D、∠AED=∠CFB |
考点:平行四边形的判定与性质
专题:
分析:根据平行四边形的性质以及平行四边形的判定定理即可作出判断.
解答:解:A、∵在平行四边形ABCD中,OA=OC,OB=OD,
若AE=CF,则OE=OF,
∴四边形DEBF是平行四边形;
B、若DE与AC不垂直,则满足AC上一定有一点DM=DE,同理有一点N使BF=BN,则四边形DEBF不一定是平行四边形,则选项错误;
C、∵在平行四边形ABCD中,OB=OD,AD∥BC,
∴∠ADB=∠CBD,
若∠ADE=∠CBF,则∠DEB=∠FBO,
则△DOE和△BOF中,
,
∴△DOE≌△BOF,
∴DE=BF,
又∵DE∥BF,
∴四边形DEBF是平行四边形.故选项正确;
D、∵∠AED=∠CFB,
∴∠DEO=∠BFO,
∴DE∥BF,
在△DOE和△BOF中,
,
∴△DOE≌△BOF,
∴DE=BF,
∴四边形DEBF是平行四边形.故选项正确.
故选B.
若AE=CF,则OE=OF,
∴四边形DEBF是平行四边形;
B、若DE与AC不垂直,则满足AC上一定有一点DM=DE,同理有一点N使BF=BN,则四边形DEBF不一定是平行四边形,则选项错误;

C、∵在平行四边形ABCD中,OB=OD,AD∥BC,
∴∠ADB=∠CBD,
若∠ADE=∠CBF,则∠DEB=∠FBO,
则△DOE和△BOF中,
|
∴△DOE≌△BOF,
∴DE=BF,
又∵DE∥BF,
∴四边形DEBF是平行四边形.故选项正确;
D、∵∠AED=∠CFB,
∴∠DEO=∠BFO,
∴DE∥BF,
在△DOE和△BOF中,
|
∴△DOE≌△BOF,
∴DE=BF,
∴四边形DEBF是平行四边形.故选项正确.
故选B.
点评:本题考查了平行四边形的性质以及判定定理,正确定理是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
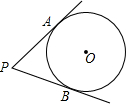 如图,已知PA、PB分别切⊙O于点A、B,∠P=60°,PA=3,那么⊙O的半径长是
如图,已知PA、PB分别切⊙O于点A、B,∠P=60°,PA=3,那么⊙O的半径长是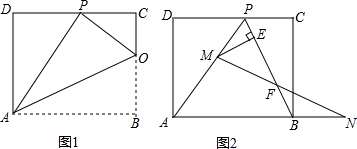 矩形ABCD一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.
矩形ABCD一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.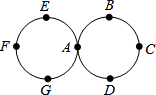 如图物体从点A出发,按照A→B(第1步)→C(第2步)→D→A→E→F→G→A→B→…的顺序循环运动,则第2015步到达点
如图物体从点A出发,按照A→B(第1步)→C(第2步)→D→A→E→F→G→A→B→…的顺序循环运动,则第2015步到达点