题目内容
10.在△ABC和△DEF中,AB=AC,DE=DF,根据下列条件,能判断△ABC和△DEF相似的是( )| A. | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | B. | $\frac{AB}{DE}$=$\frac{BC}{EF}$ | C. | ∠A=∠E | D. | ∠B=∠D |
分析 根据三组对应边的比相等的两个三角形相似判定即可.
解答 解:在△ABC和△DEF中,
∵$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$,
∴△ABC∽△DEF,
故选B.
点评 本题考查了相似三角形的判定,判定两个三角形相似有下面几种方法:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;
(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.在三角形ABC中,AB=c,BC=a,AC=b,且a、b、c满足不等式$\frac{1}{\sqrt{a-b}}$>0,$\frac{1}{\sqrt{b-c}}$>0,则a,b,c之间的大小关系为( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>a>b |
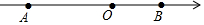 如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.
如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.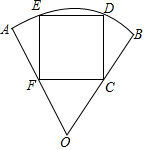 要在半径长为1米、圆心角为60°的扇形铁皮(如图)上截取一块面积尽可能大的正方形,请你设计一个截取方案(画出示意图),并计算这个正方形铁皮的面积(精确到0.01).
要在半径长为1米、圆心角为60°的扇形铁皮(如图)上截取一块面积尽可能大的正方形,请你设计一个截取方案(画出示意图),并计算这个正方形铁皮的面积(精确到0.01).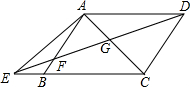 如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且$\frac{FG}{GD}$=$\frac{AD}{CE}$.
如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且$\frac{FG}{GD}$=$\frac{AD}{CE}$.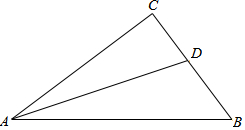 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,AD为△ABC角平分线.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,AD为△ABC角平分线. 如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A,G,H,D且∠1=∠2,∠B=∠C
如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A,G,H,D且∠1=∠2,∠B=∠C