题目内容
2.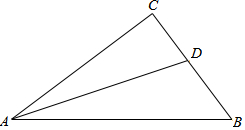 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,AD为△ABC角平分线.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,AD为△ABC角平分线.(1)用圆规在AB上作一点P,满足DP⊥AB;
(2)求:CD的长度.
分析 (1)过点D作AB的垂线,垂足为P即可;
(2)根据角平分线的性质可知∠CAD=∠BAD,利用AAS定理可知△ACD≌APD.在在Rt△ABC中根据勾股定理得出AB的长,设DP为x,则DP=x,BD=3-x,在Rt△DPB中,利用勾股定理即可得出结论.
解答 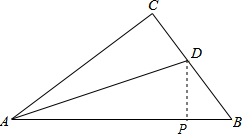 解:(1)如图,点P即为所求;
解:(1)如图,点P即为所求;
(2)∵AD平分∠BAC,
∴∠CAD=∠BAD.
又∵DC⊥AC、DP⊥AB,
∴∠C=∠APD.
在△ACD与APD中,
∵$\left\{\begin{array}{l}{∠C=∠APD}\\{∠CAD=∠BAD}\\{AD=AD}\end{array}\right.$,
∴△ACD≌APD(AAS).
∴AP=AC=4,CD=PD.
在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB=5.
设DP为x,则DP=x,BD=3-x,在Rt△DPB中,∠DPB=90°,
∴DP2+PB2=DB2,即,x2+12=(3-x)2,
解得x=$\frac{4}{3}$,
∴CD=DP=$\frac{4}{3}$.
点评 本题考查的是作图-基本作图,熟知角平分线的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在△ABC和△DEF中,AB=AC,DE=DF,根据下列条件,能判断△ABC和△DEF相似的是( )
| A. | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | B. | $\frac{AB}{DE}$=$\frac{BC}{EF}$ | C. | ∠A=∠E | D. | ∠B=∠D |
14.已知的?O直径为3cm,点P到圆心O的距离OP=2cm,则点P( )
| A. | 在?O外 | B. | 在圆?O 上 | C. | 在圆?O 内 | D. | 无法确定 |
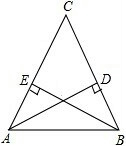 如图,从C地看A,B两地的视角∠C是锐角,从C地到A,B两地的距离相等,A地到路段BC的距离AD与B地到路段AC的距离BE相等吗?为什么?
如图,从C地看A,B两地的视角∠C是锐角,从C地到A,B两地的距离相等,A地到路段BC的距离AD与B地到路段AC的距离BE相等吗?为什么? 如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB=135度.
如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB=135度.
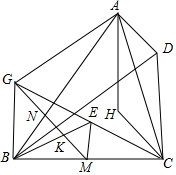 如图,已知H为锐角△ABC的垂心,D是使四边形AHCD为平行四边形的一点,过BC的中点M作AB的垂线,垂足为N,K为MN的中点,过点A作BD的平行线交MN于点G,若A,K,M,C四点共圆.求证:直线BK平分线段CG.
如图,已知H为锐角△ABC的垂心,D是使四边形AHCD为平行四边形的一点,过BC的中点M作AB的垂线,垂足为N,K为MN的中点,过点A作BD的平行线交MN于点G,若A,K,M,C四点共圆.求证:直线BK平分线段CG.