��Ŀ����
1��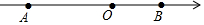 ��ͼ����������A��B���㣬AB=12��ԭ��O���߶�AB�ϵ�һ�㣬OA=2OB��
��ͼ����������A��B���㣬AB=12��ԭ��O���߶�AB�ϵ�һ�㣬OA=2OB����1��д��A��B��������ʾ��ʵ����
��2������C���߶�AB��һ�㣬������AC=CO+CB����C������ʾ��ʵ����
��3��������P��Q�ֱ��A��Bͬʱ�����������˶�����P���ٶ�Ϊÿ��2����λ���ȣ���Q���ٶ�Ϊÿ��1����λ���ȣ����˶�ʱ��Ϊt�룬����P���Q�غ�ʱ��P��Q����ֹͣ�˶���
�ٵ�tΪ��ֵʱ��2OP-OQ=4��
�ڵ���P�����Oʱ������M�ӵ�O��������ÿ��3����λ�����ٶ�Ҳ�����˶�������M�ϵ�Q���������أ���ͬ�����ٶ����P�˶���������P�����������أ���ͬ�����ٶ����Q�˶������������ֱ����P��Qֹͣʱ����MҲֹͣ�˶������ڴ˹����У���M��ʻ����·�̺͵�M���λ���������϶�Ӧ��ʵ����
���� ��1����AO=2OB��֪����12ƽ���ֳ����ݣ�AOռ����Ϊ8��OBռһ��Ϊ4����ͼ��֪��A��ԭ�����ߣ�B��ԭ����ұߣ��Ӷ��ó����ۣ�
��2��������������ٵ�C��ԭ�����ߣ������߶�OA��ʱ���ڵ�C��ԭ����ұߣ������߶�OB��ʱ���ֱ����AC=CO+CB��ʽ���ɣ�
��3���ٷ������������P��ԭ��������Ҳ�ʱ��OP��ʾ�Ĵ���ʽ��ͬ��OQ=4+t���ֱ����2OP-OQ=4��ʽ�������t��ֵ��
�ڵ�M�˶���ʱ����ǵ�P�ӵ�O��ʼ������Q��ʱ�䣬���M�˶���ʱ��Ϊt�룬��ʽΪt��2-1��=8��������ɽ�����⣮
���  �⣺��1����AB=12��AO=2OB��
�⣺��1����AB=12��AO=2OB��
��AO=8��OB=4��
��A������ʾ��ʵ��Ϊ-8��B������ʾ��ʵ��Ϊ4��
��2����C������ʾ��ʵ��Ϊx��
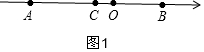
������������ٵ�C���߶�OA��ʱ����x��0����ͼ1��
��AC=CO+CB��
��8+x=-x+4-x��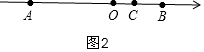
3x=-4��
x=-$\frac{4}{3}$��
�ڵ�C���߶�OB��ʱ����x��0����ͼ2��
��AC=CO+CB��
��8+x=4��
x=-4�����������⣬�ᣩ��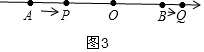
����������C������ʾ��ʵ����-$\frac{4}{3}$��
��3���ٵ�0��t��4ʱ����ͼ3��
AP=2t��OP=8-2t��BQ=t��OQ=4+t��
��2OP-OQ=4��
��2��8-2t��-��4+t��=4��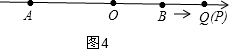
t=$\frac{8}{5}$=1.6��
����P���Q�غ�ʱ����ͼ4��
2t=12+t��t=12��
��4��t��12ʱ����ͼ5��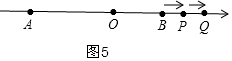
OP=2t-8��OQ=4+t��
��2��2t-8��-��4+t��=4��
t=8��
������������tΪ1.6���8��ʱ��2OP-OQ=4��
�ڵ���P�����Oʱ��8��2=4����ʱ��OQ=4+t=8������Q����ʾ��ʵ��Ϊ8��
��ͼ6�����M�˶���ʱ��Ϊt�룬
������ã�2t-t=8��
t=8��
��ʱ����P��ʾ��ʵ��Ϊ8��2=16�����Ե�M��ʾ��ʵ��Ҳ��16��
���M��ʻ����·��Ϊ��3��8=24��
�𣺵�M��ʻ����·��Ϊ24�͵�M���λ���������϶�Ӧ��ʵ��Ϊ16��
���� ���⿼��������������ľ��롢�����ϵ�ı�ʾ��һԪһ�η��̵�Ӧ�ã��Ƚϸ��ӣ�Ҫ�����������⣬��ע�������ϵĵ㣬ԭ����߱�ʾ�������ұ߱�ʾ�������������ϣ�����ľ���������������ʾ�����IJ�ľ���ֵ��

 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д� ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�| A�� | 3a2bc��bca2����ͬ���� | B�� | $\frac{{m}^{2}n}{5}$��$\frac{a+b}{2}$���ǵ���ʽ | ||
| C�� | ����ʽ-x3y2�Ĵ�����3��ϵ����-1 | D�� | 3x2-y+2xy2����������ʽ |
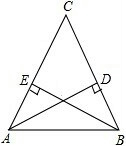 ��ͼ����C�ؿ�A��B���ص��ӽǡ�C����ǣ���C�ص�A��B���صľ�����ȣ�A�ص�·��BC�ľ���AD��B�ص�·��AC�ľ���BE�����Ϊʲô��
��ͼ����C�ؿ�A��B���ص��ӽǡ�C����ǣ���C�ص�A��B���صľ�����ȣ�A�ص�·��BC�ľ���AD��B�ص�·��AC�ľ���BE�����Ϊʲô�� | A�� | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | B�� | $\frac{AB}{DE}$=$\frac{BC}{EF}$ | C�� | ��A=��E | D�� | ��B=��D |
| A�� | ��?O�� | B�� | ��Բ?O �� | C�� | ��Բ?O �� | D�� | ��ȷ�� |

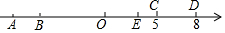 ��ͼ����������A��B��C��D��O����㣬��OΪԭ�㣬��C�������ϱ�ʾ������5���߶�CD�ij���Ϊ3����λ���߶�AB�ij���Ϊ1����λ����B��C����֮��ľ���Ϊ12����λ�������������⣺
��ͼ����������A��B��C��D��O����㣬��OΪԭ�㣬��C�������ϱ�ʾ������5���߶�CD�ij���Ϊ3����λ���߶�AB�ij���Ϊ1����λ����B��C����֮��ľ���Ϊ12����λ�������������⣺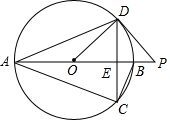 ��֪����ͼ��AB�ǡ�O��ֱ����CD���ң���AB��CD��E��P��AB�ӳ�����һ�㣬����PD����PDC=��CAD��
��֪����ͼ��AB�ǡ�O��ֱ����CD���ң���AB��CD��E��P��AB�ӳ�����һ�㣬����PD����PDC=��CAD��