题目内容
11.方程2x2-5|x|+2=0的根为( )| A. | x=±2 | B. | $x=±\frac{1}{2}$ | C. | x=±2或x=±$\frac{1}{2}$ | D. | 不能确定 |
分析 把方程看作关于|x|的一元二次方程,然后利用因式分解法解方程即可.
解答 解:2|x|2-5|x|+2=0,
(2|x|-1)(|x|-2|=0,
2|x|-1=0或|x|-2=0,
所以x1=$\frac{1}{2}$,x2=-$\frac{1}{2}$,x3=2,x4=-2.
故选C.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
相关题目
 若E是?ABCD内任意一点,若?ABCD的面积是6,则阴影部分面积是3.
若E是?ABCD内任意一点,若?ABCD的面积是6,则阴影部分面积是3.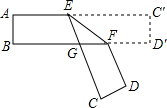 如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( )
如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( ) 如图所示,已知AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF,试说明AE与CF相等.
如图所示,已知AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF,试说明AE与CF相等.