题目内容
3.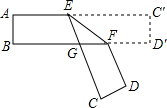 如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( )
如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( )(1)∠C′EF=32°(2)∠AEC=116°(3)∠BGE=64° (4)∠BFD=116°.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据平行线的性质由AC′∥BD′,得到∠C′EF=∠EFB=32°;根据折叠的性质得∠C′EF=∠FEC,则∠C′EC=2×32°=64°,利用平角的定义得到∠AEC=180°-64°=116°;再根据折叠性质有∠BFD=∠EFD′,利用平角的定义得到∠BFD=∠EFD′-∠BFE=180°-2∠EFB=180°-64°=116°;根据平行线性质可得∠BGE=∠C′EC=2×32°.
解答 解:∵AC′∥BD′,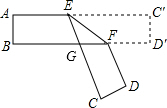
∴∠C′EF=∠EFB=32°,所以(1)正确;
∵∠C′EF=∠FEC,
∴∠C′EC=2×32°=64°,
∴∠AEC=180°-64°=116°,所以(2)正确;
∴∠BFD=∠EFD′-∠BFE=180°-2∠EFB=180°-64°=116°,所以(4)正确;
∠BGE=∠C′EC=2×32°=64°,所以(3)正确.
故选D.
点评 本题考查的是平行线的性质及翻折变换的性质,熟知图形翻折不变性的性质是解答此题的关键.

练习册系列答案
相关题目
11.方程2x2-5|x|+2=0的根为( )
| A. | x=±2 | B. | $x=±\frac{1}{2}$ | C. | x=±2或x=±$\frac{1}{2}$ | D. | 不能确定 |
18.两数相加,和小于每一个加数,那么这两个数是( )
| A. | 同为正数 | B. | 同为负数 | ||
| C. | 一正一负 | D. | 一个为0,另一个为正 |
15.若|a|=1,b2=16,且ab<0,则a+b等于( )
| A. | 5 | B. | -5 | C. | 3 | D. | ±3 |
13.关于x的方程(m2-m)x2+mx+1=0是一元二次方程的条件是( )
| A. | m≠1 | B. | m≠0 | C. | m≠1且m≠0 | D. | 无法确定 |
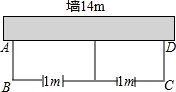 如图,有长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料造了宽为1米的两个小门.
如图,有长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料造了宽为1米的两个小门.