题目内容
1.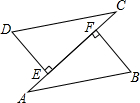 如图所示,已知AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF,试说明AE与CF相等.
如图所示,已知AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF,试说明AE与CF相等.某合作学习小组的两名同学的解题过程如下:
学生甲:因为DE⊥AC,BF⊥AC,所以∠DEC=∠BFA=90°,在Rt△ABF与Rt△CDE中,$\left\{\begin{array}{l}{AB=CD}\\{DE=BF}\end{array}\right.$,所以Rt△ABF≌Rt△CDE(HL),所以AE=FC(全等三角形的对应边相等).
学生乙:因为DE⊥AC,BF⊥AC,所以∠DEC=∠BFA=90°,在Rt△DEC和Rt△BFA中,$\left\{\begin{array}{l}{DC=BA}\\{DE=BF}\end{array}\right.$,所以Rt△DEC≌Rt△BFA(HL),所以EC=FA(全等三角形的对应边相等),所以EC-EF=AF-EF,即CF=AE,请你分析以上两种解答过程,判断谁对谁错,并指出错误的原因.
分析 认真审题可以发现,题目提供的条件是两个三角形都是直角三角形,而且知道,这两个直角三角形的一条直角边和一条斜边分别相等,所以可以根据“HL”定理判定这两个直角三角形全等,然后得出EC=FA,据此对甲、乙两个学生的解答思路进行分析即可.
解答 解:∵DE⊥AC,BF⊥AC,∴∠DEC=∠BFA=90°,
在Rt△DEC和Rt△BFA中,
$\left\{\begin{array}{l}{DC=BA}\\{DE=BF}\end{array}\right.$,
∴Rt△DEC≌Rt△BFA(HL),
∴EC=FA,
∴EC-EF=AF-EF,
即CF=AE,
由上可知,学生乙的解答过程正确,
学生甲的解答过程错误,
错误有两个,
①在Rt△ABF与Rt△CDE中,$\left\{\begin{array}{l}{AB=CD}\\{DE=BF}\end{array}\right.$应改为$\left\{\begin{array}{l}{AB=CD}\\{BF=DE}\end{array}\right.$,
②由Rt△ABF≌Rt△CDE得到的直接结果是:EC=FA.
点评 本题主要考查了直角三角形的判定定理,即:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等,注意总结.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
11.方程2x2-5|x|+2=0的根为( )
| A. | x=±2 | B. | $x=±\frac{1}{2}$ | C. | x=±2或x=±$\frac{1}{2}$ | D. | 不能确定 |
13.关于x的方程(m2-m)x2+mx+1=0是一元二次方程的条件是( )
| A. | m≠1 | B. | m≠0 | C. | m≠1且m≠0 | D. | 无法确定 |
 观察下列每对数在数轴上的对应点间的距离:4与7,3与-5,-2与-5,0与-3
观察下列每对数在数轴上的对应点间的距离:4与7,3与-5,-2与-5,0与-3
 如图,长方形ABCD中,AB=4,BC=5,将长方形沿折痕AF折叠,点D恰好落在BC边上的点E处.
如图,长方形ABCD中,AB=4,BC=5,将长方形沿折痕AF折叠,点D恰好落在BC边上的点E处.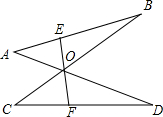 如图,AD、BC相交于点O,且OA=OC,OB=OD,EF过点O,分别交AB、CD于点E、F,且∠AOE=∠COF,求证:OE=OF.
如图,AD、BC相交于点O,且OA=OC,OB=OD,EF过点O,分别交AB、CD于点E、F,且∠AOE=∠COF,求证:OE=OF.