题目内容
5.(1)已知|a-2|+b2-2b+1=0,则a=2,b=1;(2)若x2-4x+y2+2y+5=0,则x=2,y=-1.
分析 根据配方法把原式化为非负数的和的形式,根据非负数的性质解答即可.
解答 解:(1)∵|a-2|+b2-2b+1=0,
∴|a-2|+(b-1)2=0,
∴a-2=0,b-1=0,
解得a=2,b=1.
故答案为:2;1;
(2)∵x2-4x+y2+2y+5=0,
∴(x-2)2+(y+1)2=0,
∴x-2=0,y+1=0,
解得x=2,y=-1.
故答案为:2;-1.
点评 本题考查的是配方法的应用、非负数的性质,掌握配方法的一般步骤和当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.

练习册系列答案
相关题目
15.在下列多项式中,有相同因式的是( )
①x2+5x+6 ②x2+4x+3 ③x2+6x+8 ④x2-2x-15 ⑤x2-x-20.
①x2+5x+6 ②x2+4x+3 ③x2+6x+8 ④x2-2x-15 ⑤x2-x-20.
| A. | 只有①⑤ | B. | 只有②④ | C. | 只有③⑤ | D. | 以上答案均不对 |
 如图所示,点O在直线AE上,CO平分∠AOE,∠DOB是直角,则∠1的余角为∠DOE和∠BOC.
如图所示,点O在直线AE上,CO平分∠AOE,∠DOB是直角,则∠1的余角为∠DOE和∠BOC.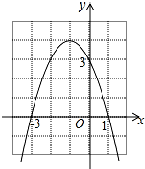 如图是二次函数y=ax2+bx+c的图象,下列结论:
如图是二次函数y=ax2+bx+c的图象,下列结论: