题目内容
18.有一道题:“先化简?($\frac{m}{m+1}$-$\frac{2}{{m}^{2}-1}$)÷($\frac{1}{m-1}$+1)再其求值.”小王代入某个数后,求得值为-1,你能确定小王代入的是哪一个值吗?你认为他代入的值合适吗?请说明理由.
分析 先算括号里面的,再算除法,再令代数式的值为-1,求出m的值即可.
解答 解:不合适.
理由:原式=$\frac{{m}^{2}-m-2}{(m+1)(m-1)}$÷$\frac{1+m-1}{m-1}$
=$\frac{(m+1)(m-2)}{(m+1)(m-1)}$•$\frac{m-1}{m}$
=$\frac{m-2}{m-1}$•$\frac{m-1}{m}$
=$\frac{m-2}{m}$,
∵代入某个数后,求得值为-1,
∴$\frac{m-2}{m}$=-1,解得m=1,
当m=1时,代数式无意义.
点评 本题考查的是分式的化简求出,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
相关题目
3.下列方程的解为x=1的是( )
| A. | $\frac{x-1}{2}$=10 | B. | 2-x=2x-1 | C. | $\frac{2}{x}$+1=0 | D. | x2=2 |
7.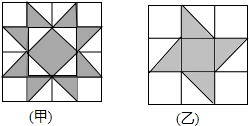 如图是甲、乙两种地板,它们都是由等腰直角三角形和正方形的地砖拼成,且直角边与正方形边的长相等,一个小球分别在这两种地板上自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则P1与P2的大小关系是( )
如图是甲、乙两种地板,它们都是由等腰直角三角形和正方形的地砖拼成,且直角边与正方形边的长相等,一个小球分别在这两种地板上自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则P1与P2的大小关系是( )
 如图是甲、乙两种地板,它们都是由等腰直角三角形和正方形的地砖拼成,且直角边与正方形边的长相等,一个小球分别在这两种地板上自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则P1与P2的大小关系是( )
如图是甲、乙两种地板,它们都是由等腰直角三角形和正方形的地砖拼成,且直角边与正方形边的长相等,一个小球分别在这两种地板上自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则P1与P2的大小关系是( )| A. | P1<P2 | B. | P1=P2 | C. | P1>P2 | D. | 无法确定 |
8.估计$\sqrt{31}$的值( )
| A. | 在6和7之间 | B. | 在5和6之间 | C. | 在3和4之间 | D. | 在2和3之间 |
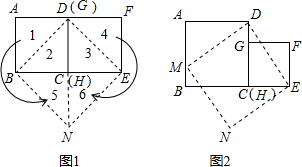
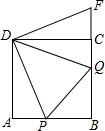 如图,在边长为8cm的正方形ABCD中,动点P从点A出发,沿线段AB以每秒1cm的速度向点B运动;同时动点Q从点B出发,沿线段BC以每秒3cm的速度向点C运动.当点Q到达C点时,点P同时停止,设运动时间为t秒.
如图,在边长为8cm的正方形ABCD中,动点P从点A出发,沿线段AB以每秒1cm的速度向点B运动;同时动点Q从点B出发,沿线段BC以每秒3cm的速度向点C运动.当点Q到达C点时,点P同时停止,设运动时间为t秒.