题目内容
观察下列各式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1;
…
(1)根据上面各式的规律可得(x-1)(xn+xn-1+…+x2+x+1)= (其中n为正整数);
(2)利用上述规律,求1+2+22+23+…+250的值.
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1;
…
(1)根据上面各式的规律可得(x-1)(xn+xn-1+…+x2+x+1)=
(2)利用上述规律,求1+2+22+23+…+250的值.
考点:多项式乘多项式
专题:规律型
分析:(1)根据已知等式,归纳总结得到一般性结果即可;
(2)原式变形后,计算即可得到结果.
(2)原式变形后,计算即可得到结果.
解答:解:(1)(x-1)(xn+xn-1+…+x2+x+1)=xn+1-1;
(2)原式=(2-1)(1+2+22+23+…+250)=251-1.
故答案为:(1)xn+1-1.
(2)原式=(2-1)(1+2+22+23+…+250)=251-1.
故答案为:(1)xn+1-1.
点评:此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知⊙O的半径是3,点O到直线l的距离为1,则直线l与⊙O的位置关系是( )
| A、相离 | B、相切 |
| C、相交 | D、无法判断 |
 在△ABC中,AB=AC=10cm,BC=12cm,以点B为圆心,8cm长为半径的圆与AC有怎样的位置关系?
在△ABC中,AB=AC=10cm,BC=12cm,以点B为圆心,8cm长为半径的圆与AC有怎样的位置关系? 如图,AB、BC、CD分别与半圆O相切于A、E、D三点,若AB=4,CD=9,求半圆O的半径.
如图,AB、BC、CD分别与半圆O相切于A、E、D三点,若AB=4,CD=9,求半圆O的半径.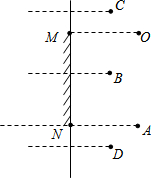 如图所示,一面镜子MN竖直悬挂在墙壁上,人眼O的位置与镜子MN上沿M处于同一水平线. 有四个物体A、B、C、D放在镜子前面,人眼能从镜子看见的物体有
如图所示,一面镜子MN竖直悬挂在墙壁上,人眼O的位置与镜子MN上沿M处于同一水平线. 有四个物体A、B、C、D放在镜子前面,人眼能从镜子看见的物体有