题目内容
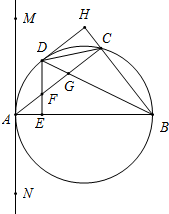 如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.(1)求证:MN是半圆的切线;
(2)作DH⊥BC交BC的延长线于点H,连接CD,试判断线段AE与线段CH的数量关系,并说明理由.
(3)若BC=4,AB=6,试求AE的长.
考点:切线的判定
专题:
分析:(1)由AB是直径得出∠ACB=90°,推出∠CAB+∠MAC=90°即可;
(2)连接AD,证明△ADE≌△CDH即可;
(3)由(2)可得出AE=CH,且DE=DH,可证得BE=BH,结合BC和AB的长可求出AE.
(2)连接AD,证明△ADE≌△CDH即可;
(3)由(2)可得出AE=CH,且DE=DH,可证得BE=BH,结合BC和AB的长可求出AE.
解答: 解:(1)如右图所示,
解:(1)如右图所示,
∵AB是直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
∵∠MAC=∠ABC,
∴∠CAB+∠MAC=90°,
即∠MAB=90°,
∴MN是半圆的切线;
(2)AE=CH,理由如下:
连接AD,
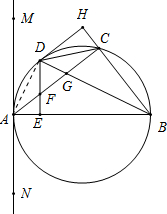
∵D是
的中点,
∴AD=CD,∠HBD=∠ABD,
∵DE⊥AB,DH⊥BC,
∴AD=DC,且∠AED=∠DHC,
在Rt△ADE和Rt△CDH中,
,
∴Rt△ADE≌Rt△CDH(HL),
∴AE=CH;
(3)由(2)知DH=DE,∠DHB=∠DEB=90°,
在△RtDBH和Rt△DBE中,
,
∴△RtDBH≌Rt△DBE(HL),
∴BE=BH,
∴BA-AE=BC+CH,且AE=CH,
∴BA-AE=BC+AE,
又∵AB=6,BC=4,
∴6-AE=4+AE,
∴AE=1.
 解:(1)如右图所示,
解:(1)如右图所示,∵AB是直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
∵∠MAC=∠ABC,
∴∠CAB+∠MAC=90°,
即∠MAB=90°,
∴MN是半圆的切线;
(2)AE=CH,理由如下:
连接AD,

∵D是
 |
| AC |
∴AD=CD,∠HBD=∠ABD,
∵DE⊥AB,DH⊥BC,
∴AD=DC,且∠AED=∠DHC,
在Rt△ADE和Rt△CDH中,
|
∴Rt△ADE≌Rt△CDH(HL),
∴AE=CH;
(3)由(2)知DH=DE,∠DHB=∠DEB=90°,
在△RtDBH和Rt△DBE中,
|
∴△RtDBH≌Rt△DBE(HL),
∴BE=BH,
∴BA-AE=BC+CH,且AE=CH,
∴BA-AE=BC+AE,
又∵AB=6,BC=4,
∴6-AE=4+AE,
∴AE=1.
点评:本题主要考查切线的判定及圆周角定理等知识的综合运用,注意证明切线的两种思路,已知切点时可证明垂直,没有切点时可作垂直证明距离等于半径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
把下列各数填在相应的大括号内:
-5,|-
|,-12,0,-3.14,+1.99,-(-6),
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
-5,|-
| 3 |
| 4 |
| 22 |
| 7 |
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
 如图,一圆柱高8cm,底面半径为
如图,一圆柱高8cm,底面半径为| 6 |
| π |
| A、6cm | B、8cm |
| C、10cm | D、12cm |
 如图,在△ABC中,D、E分别是AB、AC的中点,F是BC延长线上的一点,FC=3,DF交CE于点G,且EG=CG,则BC=
如图,在△ABC中,D、E分别是AB、AC的中点,F是BC延长线上的一点,FC=3,DF交CE于点G,且EG=CG,则BC=
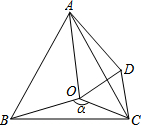 如图,已知点O是等边AO=AD内一点,∠BOC=α,且OC=3.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,则OD=
如图,已知点O是等边AO=AD内一点,∠BOC=α,且OC=3.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,则OD=