题目内容
二次函数y=ax2+bx+c的最大值为
,其图象经过A(0,-2),B(5,-2).若点C在x轴上,∠ACB=90°,且CA<CB,△ABC绕点A逆时针旋转,使点C的对应点C′落在x轴上.
(1)求二次函数的解析式;
(2)求点B的对应点B′的坐标并判断是否在该二次函数上.
| 13 |
| 6 |
(1)求二次函数的解析式;
(2)求点B的对应点B′的坐标并判断是否在该二次函数上.
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征
专题:
分析:解:(1)根据待定系数法,可得函数解析式;
(2)根据旋转的性质,可得旋转角相等,根据互余锐角三角函数的关系,可得∠B′CO的三角函数,根据三角函数的定义,可得点B′的坐标,根据把点的坐标代入函数解析式,可得答案.
(2)根据旋转的性质,可得旋转角相等,根据互余锐角三角函数的关系,可得∠B′CO的三角函数,根据三角函数的定义,可得点B′的坐标,根据把点的坐标代入函数解析式,可得答案.
解答:解:(1)由题意,得
解得
,
二次函数的解析式是y=-
x2+
x-2;
(2)如图:
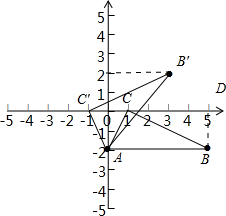 ,
,
设C点坐标是(x,0),由勾股定理,得
AC2=x2+(-2)2,BC2=(5-x)2+(-2)2,
AC2+BC2=AB2,
即[x2+(-2)2][(5-x)2+(-2)2]=25,
解得x=1或x=4(不符合题意的要舍去),
C(1,0).
由旋转的性质,得
∠C′AC=∠B′AB,AB′=AB=5.
sin∠CAO=
,cos∠CAO=
,
sin∠CAC′=2sin∠CAO•cos∠CAO=2×
×
=
,
cos∠CAC′=
,
∴sin∠BOB′=sin∠CAC′=
,cos∠CAC′=
.
由锐角的余角的三角函数关系,得
sin∠B′AE=cos∠CAC′=
,cos∠B′AE=sin∠CAC′=
,
AD=5×cos∠B′AE=5×
=4,EO=EA-AO=2.
B′D=5×sin∠B′AE=5×
=3,
B′(3,2),
把B′(3,2)代入y=-
x2+
x-2;
左边=2,右边=-
×32+
×3-2=5,
左边≠右边,
点B′的坐标不在该二次函数上.
|
解得
|
二次函数的解析式是y=-
| 2 |
| 3 |
| 10 |
| 3 |
(2)如图:
 ,
,设C点坐标是(x,0),由勾股定理,得
AC2=x2+(-2)2,BC2=(5-x)2+(-2)2,
AC2+BC2=AB2,
即[x2+(-2)2][(5-x)2+(-2)2]=25,
解得x=1或x=4(不符合题意的要舍去),
C(1,0).
由旋转的性质,得
∠C′AC=∠B′AB,AB′=AB=5.
sin∠CAO=
| ||
| 5 |
2
| ||
| 5 |
sin∠CAC′=2sin∠CAO•cos∠CAO=2×
| ||
| 5 |
2
| ||
| 5 |
| 4 |
| 5 |
cos∠CAC′=
| 3 |
| 5 |
∴sin∠BOB′=sin∠CAC′=
| 4 |
| 5 |
| 3 |
| 5 |
由锐角的余角的三角函数关系,得
sin∠B′AE=cos∠CAC′=
| 3 |
| 5 |
| 4 |
| 5 |
AD=5×cos∠B′AE=5×
| 4 |
| 5 |
B′D=5×sin∠B′AE=5×
| 3 |
| 5 |
B′(3,2),
把B′(3,2)代入y=-
| 2 |
| 3 |
| 13 |
| 6 |
左边=2,右边=-
| 2 |
| 3 |
| 13 |
| 3 |
左边≠右边,
点B′的坐标不在该二次函数上.
点评:本题考查了待定系数法求二次函数解析式,利用了待定系数法求解析式 利用了点的坐标满足函数解析式,求解B′点的坐标是解题关键.

练习册系列答案
相关题目
2的绝对值是( )
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
在Rt△ABC中,∠ACB=90°,AC=6,AB=10,以C为圆心,BC为半径作⊙C,则点A与⊙C的位置关系是( )
| A、点A在⊙C内 |
| B、点A在⊙C上 |
| C、点A在⊙C外 |
| D、无法确定 |
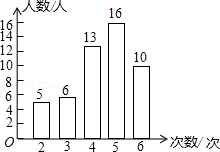 (1)某市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题;
(1)某市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题;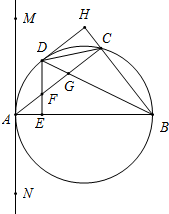 如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.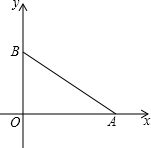 如图,已知A(8,0),B(0,6),两个动点P、Q同时在△OAB的边上按逆时针方向(→O→A→B→O→)运动,开始时点P在点B位置,点Q在点O位置,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位.
如图,已知A(8,0),B(0,6),两个动点P、Q同时在△OAB的边上按逆时针方向(→O→A→B→O→)运动,开始时点P在点B位置,点Q在点O位置,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位. 如图,在△ABC中,AD、CE都是高,且有AD=CE.求证:AB=BC.
如图,在△ABC中,AD、CE都是高,且有AD=CE.求证:AB=BC.