题目内容
已知二次函数y=ax2+bx+c(a≠0)的图象经过一次函数y=-
x+3的图象与x轴、y轴的交点,同时经过(1,1)点.求这个二次函数解析式,并求x为何值时,有最大(最小)值,这个值是什么?
| 3 |
| 2 |
考点:二次函数的性质,二次函数的最值
专题:
分析:由题意先设出二次函数的解析式:y=ax2+bx+c,一次函数y=-
x+3的图象与x轴、y轴的交点在二次函数图象上,分别令一次函数x=0,y=0求出其与x轴、y轴的交点,再根据点(1,1)也在二次函数图象上,把三点代入二次函数的解析式,用待定系数法求出二次函数的解析式,配方后即可确定最值.
| 3 |
| 2 |
解答:解:由y=-
x+3的图象与x轴、y轴的交点,并且经过点(1,1),
令x=0,得y=3;
令y=0,得x=2
∴二次函数图象经过(0,3),(2,0),(1,1)三点,
把(0,3),(2,0),(1,1)分别代入y=ax2+bx+c,
得
,
解得
,
∴二次函数关系式为y=
x2-
x+3=
(x-
)2-
.
∴当x=
时有最小值为-
.
| 3 |
| 2 |
令x=0,得y=3;
令y=0,得x=2
∴二次函数图象经过(0,3),(2,0),(1,1)三点,
把(0,3),(2,0),(1,1)分别代入y=ax2+bx+c,
得
|
解得
|
∴二次函数关系式为y=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 8 |
∴当x=
| 5 |
| 2 |
| 1 |
| 8 |
点评:此题主要考查一次函数和二次函数的基本性质,一次函数与x轴、y轴的交点坐标,用待定系数法求出二次函数的解析式.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 下列不等式组中,它的解集在数轴上表示成如图所示,则这个不等式组为( )
下列不等式组中,它的解集在数轴上表示成如图所示,则这个不等式组为( )A、
| |||||
B、
| |||||
C、
| |||||
D、
|
在Rt△ABC中,∠ACB=90°,AC=6,AB=10,以C为圆心,BC为半径作⊙C,则点A与⊙C的位置关系是( )
| A、点A在⊙C内 |
| B、点A在⊙C上 |
| C、点A在⊙C外 |
| D、无法确定 |
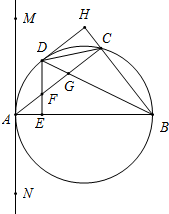 如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.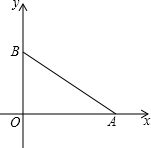 如图,已知A(8,0),B(0,6),两个动点P、Q同时在△OAB的边上按逆时针方向(→O→A→B→O→)运动,开始时点P在点B位置,点Q在点O位置,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位.
如图,已知A(8,0),B(0,6),两个动点P、Q同时在△OAB的边上按逆时针方向(→O→A→B→O→)运动,开始时点P在点B位置,点Q在点O位置,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位.