题目内容
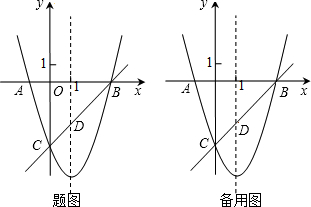
如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交y轴于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ=
AB时,求CE的长;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交y轴于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ=
| 3 |
| 4 |
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.

考点:二次函数综合题
专题:
分析:(1)利用对称轴公式即可得出b的值,再利用抛物线与y轴交于点C(0,-3),求出抛物线解析式即可;
(2)由抛物线解析式得到B、C点坐标,即可得到直线BC的函数表达式;
(3)①由抛物线的对称性可得PM=
,可得P点坐标,进而得出F点坐标以及FC的长度,根据垂直平分的性质即可得出CE的长度;
②当∠CDE=90°时,则CE为斜边,则DG2=CG•GE,即1=(OC-OG)•(2-a),求出a的值,进而得出P点坐标;当CD为斜边时,DE⊥CE,可得到P和F的纵坐标为-
,代入抛物线解析式,可得P点坐标.
(2)由抛物线解析式得到B、C点坐标,即可得到直线BC的函数表达式;
(3)①由抛物线的对称性可得PM=
| 3 |
| 2 |
②当∠CDE=90°时,则CE为斜边,则DG2=CG•GE,即1=(OC-OG)•(2-a),求出a的值,进而得出P点坐标;当CD为斜边时,DE⊥CE,可得到P和F的纵坐标为-
| 5 |
| 2 |
解答:解:(1)∵抛物线的对称轴为直线x=1,
∴-
=-
=1.
∴b=-2.
∵抛物线与y轴交于点C(0,-3),
∴c=-3.
∴抛物线的函数表达式为y=x2-2x-3;
(2)∵抛物线与x轴交于A、B两点,
当y=0时,x2-2x-3=0.
∴x1=-1,x2=3.
∵A点在B点左侧,
∴A(-1,0),B(3,0).
设过点B(3,0)、C(0,-3)的直线的函数表达式为y=kx+m,
则
,
∴
,
∴直线BC的函数表达式为:y=x-3;
(3)①∵AB=4,PQ=
AB,
∴PQ=3.
∵PQ⊥y轴,
∴PQ∥x轴.
则由抛物线的对称性可得PM=
,
∵对称轴是直线x=1,
∴P到y轴的距离是
.
∴点P的横坐标为-
.
∴P(-
,-
).
∴F(0,-
).
∴FC=3-OF=3-
=
.
∵PQ垂直平分CE于点F,
∴CE=2FC=
.
②P1(1-
,-2),P2(1-
,-
).
设OE=a,则GE=2-a,
∵当CE为斜边时,
∴DG2=CG•GE,即1=(OC-OG)•(2-a),
∴1=1×(2-a).
∴a=1.
∴CE=2.
∴OF=OE+EF=2.
∴F、P的纵坐标为-2.
把y=-2,代入抛物线的函数表达式为y=x2-2x-3得:x=1+
或1-
∵点P在第三象限,
∴P1(1-
,-2).
∵当CD为斜边时,DE⊥CE,
∴OE=2,CE=1.
∴OF=2.5.
∴P和F的纵坐标为:-
.
把y=-
,代入抛物线的函数表达式为y=x2-2x-3得:x=1-
,或1+
,
∵点P在第三象限,
∴P2(1-
,-
).
综上所述:满足条件为P1(1-
,-2),P2(1-
,-
).
∴-
| b |
| 2a |
| b |
| 2×1 |
∴b=-2.
∵抛物线与y轴交于点C(0,-3),
∴c=-3.
∴抛物线的函数表达式为y=x2-2x-3;
(2)∵抛物线与x轴交于A、B两点,
当y=0时,x2-2x-3=0.
∴x1=-1,x2=3.
∵A点在B点左侧,
∴A(-1,0),B(3,0).
设过点B(3,0)、C(0,-3)的直线的函数表达式为y=kx+m,
则
|
∴
|
∴直线BC的函数表达式为:y=x-3;
(3)①∵AB=4,PQ=
| 3 |
| 4 |
∴PQ=3.
∵PQ⊥y轴,
∴PQ∥x轴.
则由抛物线的对称性可得PM=
| 3 |
| 2 |
∵对称轴是直线x=1,
∴P到y轴的距离是
| 1 |
| 2 |
∴点P的横坐标为-
| 1 |
| 2 |
∴P(-
| 1 |
| 2 |
| 7 |
| 4 |
∴F(0,-
| 7 |
| 4 |

∴FC=3-OF=3-
| 7 |
| 4 |
| 5 |
| 4 |
∵PQ垂直平分CE于点F,
∴CE=2FC=
| 5 |
| 2 |
②P1(1-
| 2 |
| ||
| 2 |
| 5 |
| 2 |
设OE=a,则GE=2-a,
∵当CE为斜边时,
∴DG2=CG•GE,即1=(OC-OG)•(2-a),
∴1=1×(2-a).
∴a=1.
∴CE=2.
∴OF=OE+EF=2.
∴F、P的纵坐标为-2.
把y=-2,代入抛物线的函数表达式为y=x2-2x-3得:x=1+
| 2 |
| 2 |
∵点P在第三象限,
∴P1(1-
| 2 |
∵当CD为斜边时,DE⊥CE,
∴OE=2,CE=1.
∴OF=2.5.
∴P和F的纵坐标为:-
| 5 |
| 2 |
把y=-
| 5 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∵点P在第三象限,
∴P2(1-
| ||
| 2 |
| 5 |
| 2 |
综上所述:满足条件为P1(1-
| 2 |
| ||
| 2 |
| 5 |
| 2 |
点评:本题主要考查了二次函数的综合题型、涉及直角三角形的性质和待定系数法求一次函数解析式等知识,在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
设[x]表示不超过x的最大整数,如[2.7]=2,[-4.5]=-5;计算[3.7]+[-6.5]的值为( )
| A、-2 | B、-3 | C、-4 | D、3 |
 如图,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=4,CD=5,AD=6,动点P从点A开始以每秒1个单位长度的速度向点B匀速运动,动点Q从点B开始沿折线BC-CD以每秒2个单位长度的速度向点D匀速运动,过点P作PE⊥AB,交CD于点E,设点P、Q同时开始运动,且时间为t秒(t>0),当点P与点B重合时停止运动,点Q也随之停止运动.
如图,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=4,CD=5,AD=6,动点P从点A开始以每秒1个单位长度的速度向点B匀速运动,动点Q从点B开始沿折线BC-CD以每秒2个单位长度的速度向点D匀速运动,过点P作PE⊥AB,交CD于点E,设点P、Q同时开始运动,且时间为t秒(t>0),当点P与点B重合时停止运动,点Q也随之停止运动.