题目内容
6.已知m,x,y是两两不相等的实数且满足$\sqrt{m(x-m)}$+$\sqrt{m(y-m)}$=$\sqrt{x-m}$-$\sqrt{m-y}$,求$\frac{3{x}^{2}+xy-{y}^{2}}{{x}^{2}-xy+{y}^{2}}$的值.分析 根据被开方数是非负数,确定出m=0,x=-y,代入原式即可解决问题.
解答 解:∵m,x,y是两两不相等的实数且满足$\sqrt{m(x-m)}$+$\sqrt{m(y-m)}$=$\sqrt{x-m}$-$\sqrt{m-y}$,
又∵$\left\{\begin{array}{l}{m-y≥0}\\{x-m≥0}\\{m(y-m)≥0}\\{m(x-m)≥0}\end{array}\right.$,
∴m=0,x=-y,x≠0,y≠0,
∴原式=$\frac{3{y}^{2}-{y}^{2}-{y}^{2}}{{y}^{2}+{y}^{2}+{y}^{2}}$=$\frac{1}{3}$.
点评 本题考查二次根式的性质、解题的关键是根据条件确定出m=0,x=-y,记住二次根式的被开方数是非负数这个隐含条件,属于中考常考题型.

练习册系列答案
相关题目
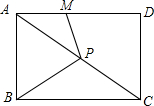 如图,点P为矩形ABCD的对角线AC上一点,PM⊥PB交AD于M.
如图,点P为矩形ABCD的对角线AC上一点,PM⊥PB交AD于M. 如数轴所示,化简:|-m-m|=-2m.
如数轴所示,化简:|-m-m|=-2m. 如图,射线BD是∠MBN的平分线,点A、C分别是角的两边BM、BN上两点,且AB=BC,E是线段BC上一点,线段EC的垂直平分线交射线BD于点F,连结AE交BD于点G,连结AF、EF、FC.
如图,射线BD是∠MBN的平分线,点A、C分别是角的两边BM、BN上两点,且AB=BC,E是线段BC上一点,线段EC的垂直平分线交射线BD于点F,连结AE交BD于点G,连结AF、EF、FC.