题目内容
5.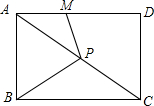 如图,点P为矩形ABCD的对角线AC上一点,PM⊥PB交AD于M.
如图,点P为矩形ABCD的对角线AC上一点,PM⊥PB交AD于M.(1)求证:$\frac{BP}{PM}$=$\frac{AD}{DC}$;
(2)若MA=MP,AB=3,BC=4,求AP的长.
分析 (1)连接BM,先证明A、B、P、M四点共圆,再证明△ADC∽△BPM即可解决问题.
(2)作BN⊥AP于N,先证明BA=BP,再求出BN、PN即可解决问题.
解答 (1)证明:连接BM.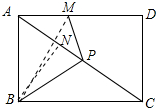 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠BAD=∠D=90°,
∵PM⊥PB,
∴∠BPM=90°,
∴∠BAM+∠BPM=180°,
∴A、B、P、M四点共圆,
∴∠MBP=∠DAC,
∵∠D=∠BPM=90°,
∴△ADC∽△BPM,
∴$\frac{AD}{PB}$=$\frac{DC}{PM}$,
∴$\frac{BP}{PM}$=$\frac{AD}{DC}$.
(2)解:作BN⊥AP于N.
在RT△BMA和RT△BMP中,
$\left\{\begin{array}{l}{BM=BM}\\{AM=PM}\end{array}\right.$,
∴△BMA≌△BMP,
∴AB=PB=3,
在RT△ABC中,∵∠ABC=90°,AB=3,BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∵$\frac{1}{2}$•AB•BC=$\frac{1}{2}$•AC•BN,
∴BN=$\frac{12}{5}$,
在RT△PBN中,PN=$\sqrt{P{B}^{2}-B{N}^{2}}$=$\frac{9}{5}$,
∵BA=BP,BN⊥AP,
∴AN=NP,
AP=2PN=$\frac{18}{5}$.
点评 本题考查矩形的性质、全等三角形的判定和性质、相似三角形的判定和性质勾股定理、四点共圆等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
7.计算(-2a2b)3(3a3b)的结果是( )
| A. | -24a8b4 | B. | -24a9b4 | C. | 24a8b4 | D. | 24a9b7 |
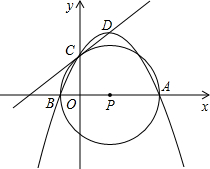 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c经过点A(4,0)、B(-1,0),与y轴交于点C,D为抛物线的顶点,过A、B、C 作⊙P.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c经过点A(4,0)、B(-1,0),与y轴交于点C,D为抛物线的顶点,过A、B、C 作⊙P.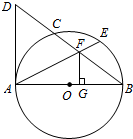 如图,AB是⊙O的直径,BD交⊙O于点C,E为 BC 的中点,连接AE交BD于点F,作FG⊥AB,垂足为G,连接AD,且∠D=2∠BAE.
如图,AB是⊙O的直径,BD交⊙O于点C,E为 BC 的中点,连接AE交BD于点F,作FG⊥AB,垂足为G,连接AD,且∠D=2∠BAE.  如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E.求证:AC是⊙O的切线.
如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E.求证:AC是⊙O的切线.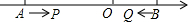 如图,数轴上的点A,B对应的数分别为-10,5.动点P,Q分别从A,B同时出发,点P以每秒3个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
如图,数轴上的点A,B对应的数分别为-10,5.动点P,Q分别从A,B同时出发,点P以每秒3个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.