题目内容
14.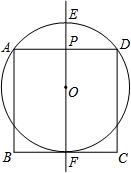 在正方形ABCD中,AD=2,l是过AD中点P的一条直线.O是l上一点,以O为圆心的圆经过点A、D,直线l与⊙O交于点E、F(E、F不与A、D重合,E在F的上面).
在正方形ABCD中,AD=2,l是过AD中点P的一条直线.O是l上一点,以O为圆心的圆经过点A、D,直线l与⊙O交于点E、F(E、F不与A、D重合,E在F的上面).(1)如图,若点F在BC上,求证:BC与⊙O相切.并求出此时⊙O的半径.
(2)若⊙O半径为$\frac{2\sqrt{3}}{3}$,请直接写出∠AED的度数.
分析 (1)连接OA、OD,如图,由点P是AD的中点,根据垂径定理的推理得OP⊥AD,再利用正方形的性质得AD∥BC,所以OP⊥BC,于是可根据切线的判定定理判断BC与⊙O相切;设⊙O的半径为r,则OF=r,PF=AB=AD=2,OP=2-r,AP=$\frac{1}{2}$AD=1,在Rt△AOP中利用勾股定理得到12+(2-r)2=r2,解得r=$\frac{5}{4}$;
(2)如图,在Rt△OAP中,利用正弦定义可求出∠AOP=60°,则∠AOD=120°,根据圆周角定理得∠AFD=$\frac{1}{2}$∠AOD=60°,再根据圆内接四边形的性质得∠AED=180°-∠AFD=120°,若当交换点E和F的位置时,∠AED=60°,于是得到∠AED的度数为120°或60°.
解答 (1)证明:连接OA、OD,如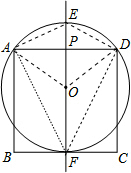 图,
图,
∵点P是AD的中点,
∴OP⊥AD,
∵四边形ABCD是正方形,
∴AD∥BC,
∴OP⊥BC,
且OF是⊙O半径,
∴BC与⊙O相切;
设⊙O的半径为r,则OF=r,
∵PF=AB=AD=2,
∴OP=2-r,
AP=$\frac{1}{2}$AD=1,
在Rt△AOP中,∵AP2+OP2=AO2,
∴12+(2-r)2=r2,解得r=$\frac{5}{4}$,
即设⊙O的半径为$\frac{5}{4}$;
(2)解:如图,在Rt△OAP中,∵sin∠AOP=$\frac{AP}{OA}$=$\frac{1}{\frac{2\sqrt{3}}{3}}$=$\frac{\sqrt{3}}{2}$,
∴∠AOP=60°,
∴∠AOD=120°,
∴∠AFD=$\frac{1}{2}$∠AOD=60°,
∴∠AED=180°-∠AFD=120°,
当交换点E和F的位置时,∠AED=60°,
∴∠AED的度数为120°或60°.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了勾股定理和正方形的性质.

| A. | -a2+2a2=3a2 | B. | 3a2×(-2a)=-6a2 | C. | a8÷a4=a2 | D. | (2a2)2=4a4 |
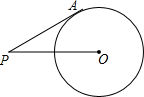 如图,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA=8,则cos∠APO等于( )
如图,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA=8,则cos∠APO等于( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
| A. | x2+3x+2 | B. | 3(x-1)(x-2) | C. | x2-3x+2 | D. | x3-3x2+2x |
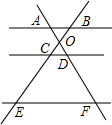 如图,已知AB∥CD∥EF,直线AF与直线BE相交于点O,下列结论错误的是( )
如图,已知AB∥CD∥EF,直线AF与直线BE相交于点O,下列结论错误的是( )| A. | $\frac{AD}{DF}=\frac{BC}{CE}$ | B. | $\frac{OA}{OC}=\frac{OB}{OD}$ | C. | $\frac{CD}{EF}=\frac{OC}{OE}$ | D. | $\frac{OA}{OF}=\frac{OB}{OE}$ |