题目内容
10.二次函数y=ax2+bx-1(a≠0)的图象经过点(1,1),则a+b+1=3.分析 先把(1,1)代入y=ax2+bx-1可得a+b的值,然后利用整体代入的方法计算a+b+1的值.
解答 解:把(1,1)代入y=ax2+bx-1得a+b-1=1,
所以a+b=2,
所以a+b+1=2+1=3.
故答案为3.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.解决此题的关键是把抛物线上点的坐标代入抛物线解析式得到a、b的等量关系.

练习册系列答案
相关题目
20.下列方程中,是二元一次方程的为( )
| A. | $x-\frac{1}{x}=3$ | B. | x+xy=-1 | C. | $\frac{x}{3}-\frac{y}{5}=6$ | D. | x2-2x-1=0 |
1.下列运算中正确的是( )
| A. | a3+a4=a12 | B. | 2(a+1)=2a+1 | C. | (-2a3)2=8a5 | D. | (3a2-a3)•a=3a3-a4 |
2. 如图,?ABCD中,AE平分∠BAD,若CE=3cm,AB=4cm,则?ABCD的周长是( )
如图,?ABCD中,AE平分∠BAD,若CE=3cm,AB=4cm,则?ABCD的周长是( )
 如图,?ABCD中,AE平分∠BAD,若CE=3cm,AB=4cm,则?ABCD的周长是( )
如图,?ABCD中,AE平分∠BAD,若CE=3cm,AB=4cm,则?ABCD的周长是( )| A. | 20cm | B. | 21cm | C. | 22cm | D. | 23cm |
 如图,两个是同心圆,弦AB与小圆相切于点C,且AB=8cm,则这个环形的面积是16πcm2.
如图,两个是同心圆,弦AB与小圆相切于点C,且AB=8cm,则这个环形的面积是16πcm2. 如图所示,小李决定星期日登A、B、C、D中的某山,打算上午9点由P地出发,尽可能去最远的山,登上山顶后休息一小时,到下午3点以前回到P地.如果去时步行的平均速度为3km/h,返回时步行的平均速度为4km/h.试问小李能登上哪个山顶?(图中数字表示由P地到能登山顶的里程)
如图所示,小李决定星期日登A、B、C、D中的某山,打算上午9点由P地出发,尽可能去最远的山,登上山顶后休息一小时,到下午3点以前回到P地.如果去时步行的平均速度为3km/h,返回时步行的平均速度为4km/h.试问小李能登上哪个山顶?(图中数字表示由P地到能登山顶的里程)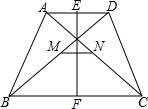 已知:如图,在梯形ABCD中,AD∥DC,AB=DC,E,F,M,N分别是AD,BC,BD,AC的中点.猜想EF与MN的关系,并证明.
已知:如图,在梯形ABCD中,AD∥DC,AB=DC,E,F,M,N分别是AD,BC,BD,AC的中点.猜想EF与MN的关系,并证明.