题目内容
1. 如图,PA,PB是圆O的切线,切点分别为A,B,若点C位圆O上一点.
如图,PA,PB是圆O的切线,切点分别为A,B,若点C位圆O上一点.(1)若∠APB=40°,则∠ACB的度数为70°.
(2)若∠APB=α°,则∠ACB的度数为90°-$\frac{1}{2}$α.
分析 连接OA、OB,如图,先根据切线的性质得∠OAP=∠OBP=90°,再根据四边形内角和得到∠AOB=180°-∠P,则根据圆周角定理得到∠ACB=$\frac{1}{2}∠$AOB=90°-$\frac{1}{2}$∠P,
(1)把∠APB=40°代入∠ACB=90°-$\frac{1}{2}$∠P计算即可;
(2)把∠APB=α代入∠ACB=90°-$\frac{1}{2}$∠P即可.
解答 解: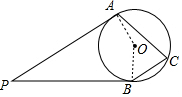 连接OA、OB,如图,
连接OA、OB,如图,
∵PA,PB是圆O的切线,
∴OA⊥AP,OB⊥PB,
∴∠OAP=∠OBP=90°,
∴∠P+∠AOB=180°,
即∠AOB=180°-∠P,
∴∠ACB=$\frac{1}{2}∠$AOB=90°-$\frac{1}{2}$∠P,
(1)当∠APB=40°,∠ACB=90°-$\frac{1}{2}$×40°=70°;
(2)∠APB=α°,∠ACB=90°-$\frac{1}{2}$α.
故答案为70°,90°-$\frac{1}{2}$α.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
 如图,AB、CD为⊙O的弦,且AB⊥CD,AB将CD分成3cm和7cm两部分,O到弦AB的距离=2cm.
如图,AB、CD为⊙O的弦,且AB⊥CD,AB将CD分成3cm和7cm两部分,O到弦AB的距离=2cm.