题目内容
7.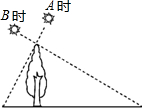 如图,小明在A时测得某树的影长为1m,B时又测得该树的影长为4米,若两次日照的光线互相垂直,树的高度为( )
如图,小明在A时测得某树的影长为1m,B时又测得该树的影长为4米,若两次日照的光线互相垂直,树的高度为( )| A. | 2m | B. | $\sqrt{3}$m | C. | $\sqrt{2}$m | D. | $\sqrt{5}$m |
分析 根据题意,画出示意图,易得:Rt△EDC∽Rt△FDC,进而可得 $\frac{ED}{DC}=\frac{DC}{FD}$,即DC2=ED•FD,代入数据可得答案.
解答 解:根据题意,作△EFC;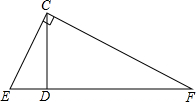
树高为CD,且∠ECF=90°,ED=4,FD=9;
易得:Rt△EDC∽Rt△FDC,
∴$\frac{ED}{DC}=\frac{DC}{FD}$;
即DC2=ED•FD,
代入数据可得DC2=4,
DC=2.
故选A.
点评 本题考查相似三角形的应用,关键是通过投影的知识结合三角形的相似,求解高的大小;是平行投影性质在实际生活中的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.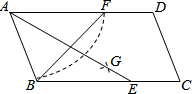 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )| A. | 16 | B. | 15 | C. | 14 | D. | 13 |
12. 如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )
如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )
 如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )
如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )| A. | $\frac{2}{3}$cm或$\frac{2}{3}\sqrt{3}$cm | B. | $\frac{2}{3}\sqrt{3}$cm | C. | $\frac{4}{3}$cm或$\frac{2}{3}\sqrt{3}$cm | D. | $\frac{2}{3}$cm或$\frac{4}{3}$cm |
19.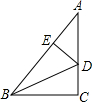 如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )
如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )
 如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )
如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )| A. | $\frac{2}{3}$cm | B. | $\frac{3}{2}$cm | C. | 2cm | D. | $\frac{3}{2}\sqrt{5}$cm |
16. 如图是一个三棱柱,它的左视图是( )
如图是一个三棱柱,它的左视图是( )
 如图是一个三棱柱,它的左视图是( )
如图是一个三棱柱,它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
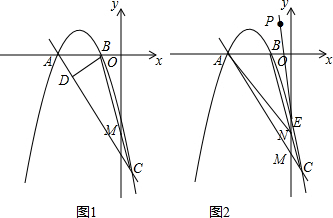
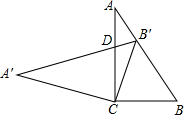 在Rt△ABC中,∠ACB=90°,cosB=$\frac{3}{5}$,将△ABC绕点C旋转后得到△A′B′C,其中B′点正好落在边AB上,A′B′交于点D,则$\frac{B′D}{CD}$的值为$\frac{7}{20}$.
在Rt△ABC中,∠ACB=90°,cosB=$\frac{3}{5}$,将△ABC绕点C旋转后得到△A′B′C,其中B′点正好落在边AB上,A′B′交于点D,则$\frac{B′D}{CD}$的值为$\frac{7}{20}$.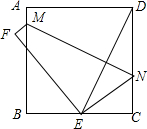 将一张边长为4cm的正方形纸片沿MN对折,使点D落在BC边上.
将一张边长为4cm的正方形纸片沿MN对折,使点D落在BC边上.