题目内容
19.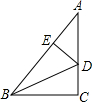 如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )
如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )| A. | $\frac{2}{3}$cm | B. | $\frac{3}{2}$cm | C. | 2cm | D. | $\frac{3}{2}\sqrt{5}$cm |
分析 首先由勾股定理求出BC,由折叠的性质可得∠BED=∠C=90°,BE=BC=3cm,得出AE=AB-BE=2cm,设DC=xcm,则DE=xcm,AD=(4-x)cm,由勾股定理得出方程,解方程即可.
解答 解:∵∠C=90°,AB=5cm,AC=4cm,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=3cm,
∵将△BCD沿着直线BD翻折,使点C落在斜边AB上的点E处,
∴△BED≌△BCD,
∴∠BED=∠C=90°,BE=BC=3cm,
∴AE=AB-BE=2cm,
设DC=xcm,则DE=xcm,AD=(4-x)cm,
由勾股定理得:AE2+DE2=AD2,
即22+x2=(4-x)2,
解得:x=$\frac{3}{2}$.
故选:B.
点评 本题主要考查翻折变换的性质,全等三角形的性质,勾股定理;熟练掌握翻折变换的性质,由勾股定理得出方程是解决问题的关键.

练习册系列答案
相关题目
9.下列调查中,适合采用全面调查的是( )
| A. | 对全国中学生心理健康现状的调查 | B. | 对某种食品合格情况的调查 | ||
| C. | 对某电视节目收视率的调查 | D. | 对你所在班级同学身高情况的调查 |
7.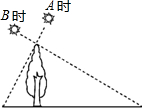 如图,小明在A时测得某树的影长为1m,B时又测得该树的影长为4米,若两次日照的光线互相垂直,树的高度为( )
如图,小明在A时测得某树的影长为1m,B时又测得该树的影长为4米,若两次日照的光线互相垂直,树的高度为( )
 如图,小明在A时测得某树的影长为1m,B时又测得该树的影长为4米,若两次日照的光线互相垂直,树的高度为( )
如图,小明在A时测得某树的影长为1m,B时又测得该树的影长为4米,若两次日照的光线互相垂直,树的高度为( )| A. | 2m | B. | $\sqrt{3}$m | C. | $\sqrt{2}$m | D. | $\sqrt{5}$m |
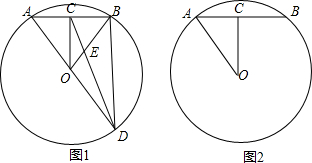
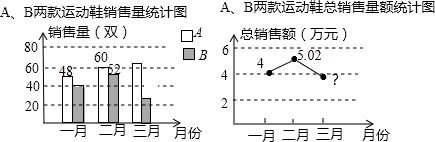
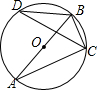 如图,AB是⊙O的直径,∠ABC=70°,则∠D的度数为20°.
如图,AB是⊙O的直径,∠ABC=70°,则∠D的度数为20°.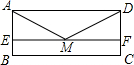 如图,矩形ABCD,E、F在AB、CD上,且EF∥AD,M为EF的中点,连接AM、DM,求证:AM=DM.
如图,矩形ABCD,E、F在AB、CD上,且EF∥AD,M为EF的中点,连接AM、DM,求证:AM=DM.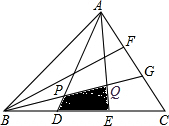 如图,△ABC的面积为1,D,E,F,G分别是BC,AC上的三等分点,求阴影四边形PQED的面积.
如图,△ABC的面积为1,D,E,F,G分别是BC,AC上的三等分点,求阴影四边形PQED的面积.