��Ŀ����
15��ͼ1�У����κ���y=-ax2-4ax-$\frac{3}{4}$��ͼ��c��x����A��B���㣨A��B����ࣩ����A���ֱ��$y=kx+3k��k��-\frac{1}{4}��$��c����һ��C��x1��y1������y����M����1�����A�����꣬������κ����Ľ���ʽ��
��2������B��BD��AC��AC��D����M��0��-3$\sqrt{3}$����Q����ֱ��AC�ϵ�һ�����㣮�������DBQ���AOM����ʱ��Q�����ꣻ
��3����P��-1��2����ͼ2����CP�����κ�����ͼ������һ��E��x2��y2������AE��y����N��OM•ON�Ƿ���һ����ֵ������Ƕ�ֵ�������ֵ�������ǣ���˵�����ɣ�
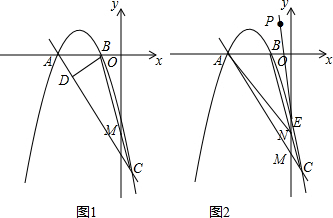
���� ��1����ֱ��y=kx+3k�����A���꣬���������߽���ʽ���ɽ�����⣮
��2���������������ۢ���ͼ1�У���Q��DA���ӳ�����ʱ����BQD=30�㣬��BQD����AOM���ڵ�Q���A�غ�ʱ����BQD=60���DQB����OAM������ͼ2�У���Q���߶�DC��ʱ����BQD=60�㣬��DQB����OAM������ͼ3�У�����BQD=30��ʱ����DQB����OMA�ֱ��ֱ�������μ��ɣ�
��3�����ֱ��PC�Ľ���ʽ������������ɷ����������E���꣬�����ֱ��AE�������N���꣬��k��ʾOM��ON���ɽ�����⣮
��� ��1���⣺y=0��kx+3k=0��֮��x=-3������A��-3��0����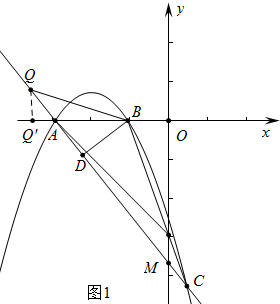
��ΪA��-3��0����y=-ax2-4ax-$\frac{3}{4}$������0=-9a+12a-$\frac{3}{4}$��
��֮�ɵ�a=$\frac{1}{4}$��
���Ըö��κ����ı���ʽy=-$\frac{1}{4}$x2-x-$\frac{3}{4}$��
��2����Rt��AOM�У�OA=3��OM=3$\sqrt{3}$tan��OAM=$\frac{OM}{AO}$=$\sqrt{3}$�����ԡ�OAM=60�㣬
����ͼ1�У���Q��DA���ӳ�����ʱ����BQD=30�㣬��BQD�ס�AOM��
��Rt��ABD��BD=BA��sin60��=$\sqrt{3}$��
��Rt��BQD��BD=OQ��sin30��=$\sqrt{3}$�����BQ=2$\sqrt{3}$��
��Q����QQ���x�ᴹ��ΪQ�䣬
�ߡ�BAD=60��=��BQA+��QBA����BQD=30�㣬
���QBQ��=30�㣬
��RT��BQQ���У��ߡ�QBQ��=30�㣬BQ=2$\sqrt{3}$��
QQ��=$\sqrt{3}$��BQ��=3��
����Q��-4��$\sqrt{3}$����
�ڵ�Q���A�غ�ʱ����BQD=60���DQB�ס�OAM���˵�Q��-3��0����
����ͼ2�У���Q���߶�DC��ʱ����BQD=60�㣬��DQB�ס�OAM��
�ڡ�AQB�У���BAQ=��AQB=60�㣬
��BQ=AB=2��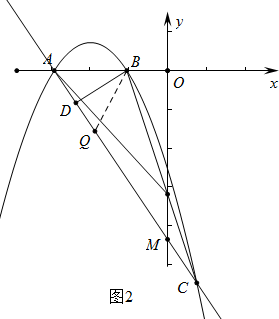
����Q��-2��-$\sqrt{3}$����
����ͼ3�У�����BQD=30��ʱ����DQB�ס�OMA����ʱBQ��OM
��Q��-1��y����ֱ��y=-$\sqrt{3}$x-3$\sqrt{3}$-�ϣ����y=-2$\sqrt{3}$��
�Ӷ�Q��-1��-2$\sqrt{3}$����
����������Q��-4��$\sqrt{3}$����Q��-3��0����Q��-2��-$\sqrt{3}$����Q��-1��-2$\sqrt{3}$����
��3����ͼ4�У�ֱ��y=kx+3k����κ���y=-$\frac{1}{4}$x2-x-$\frac{3}{4}$ͼ��Ľ�����A��C���㣬
����$\left\{\begin{array}{l}y=-\frac{1}{4}{x^2}-x-\frac{3}{4}\\ y=kx+3k\end{array}$�������ɵ�$\frac{1}{4}{x}^{2}$+��k+1��x+��$\frac{3}{4}$+3k��=0��
����ΪA��-3��0����C��x1��y1����
����x1=-4k-1��y1=-4k2+2k��
����P��-1��2�����C��ֱ�ߣ�Y=$\frac{-4{k}^{2}+2k-2}{-4k}$x+$\frac{-4{k}^{2}+2k-2}{-4k}$+2��
ֱ��PC�������ߵĽ��㣬$\left\{\begin{array}{l}{y=-\frac{1}{4}{x}^{2}-x-\frac{3}{4}}\\{y=\frac{-4{k}^{2}+2k-2}{-4k}x+\frac{-4{k}^{2}+2k-2}{-4k}+2}\end{array}\right.$����ȥy�����õ���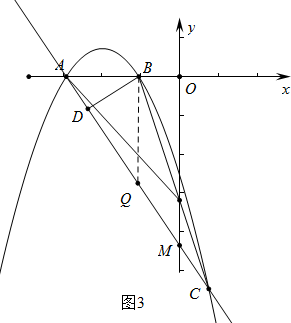
$\frac{1}{4}\\;{x}^{2}$x2+��1+$\frac{-4{k}^{2}+2k-2}{-4k}$��x+$\frac{-4{k}^{2}+2k-2}{-4k}-\frac{5}{4}$=0��
��x2+x1=x2+��-4k-1��=-$\frac{1+\frac{-4{k}^{2}+2k-2}{-4k}}{\frac{1}{4}}$��
��x2=-1-$\frac{2}{k}$��y2=$\frac{1}{k}-\frac{1}{{k}^{2}}$��
��ֱ��AEΪy=$\frac{1}{2k}$x+$\frac{3}{2k}$��
��OM=-3k��ON=-$\frac{3}{2k}$��
��OM•ON=��-3k����-$\frac{3}{2k}$��=$\frac{9}{2}$��
��OM•ON�Ƕ�ֵ�������ֵ��$\frac{9}{2}$��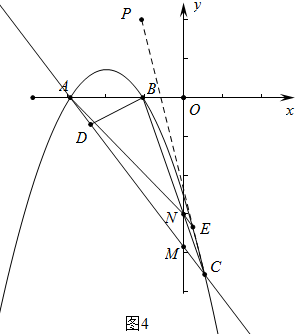
���� ���⿼����κ������й�֪ʶ�����������ε��ж������ʡ�ֱ��������30�Ƚǵ����ʵ�֪ʶ��ѧ�����ϵ����ȷ����������ʽ�ǽ���Ĺؼ���ѧ���ò�����ʾֱ�߽���ʽ��������꣬���շ������۵�˼�룬�����п�ѹ���⣮

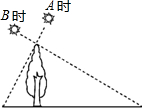 ��ͼ��С����Aʱ���ij����Ӱ��Ϊ1m��Bʱ�ֲ�ø�����Ӱ��Ϊ4�ף����������յĹ����ഹֱ�����ĸ߶�Ϊ��������
��ͼ��С����Aʱ���ij����Ӱ��Ϊ1m��Bʱ�ֲ�ø�����Ӱ��Ϊ4�ף����������յĹ����ഹֱ�����ĸ߶�Ϊ��������| A�� | 2m | B�� | $\sqrt{3}$m | C�� | $\sqrt{2}$m | D�� | $\sqrt{5}$m |
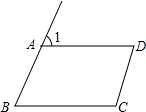 ��ͼ����B=��1����ô������ֱ��ƽ�У�ͬλ����ȣ��ɵ�AD��BC��
��ͼ����B=��1����ô������ֱ��ƽ�У�ͬλ����ȣ��ɵ�AD��BC��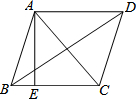 ��֪����ABCD�������Խ���AC��BD���ֱ�Ϊ6cm��8cm����AE��BC��������ε����S=24cm2��AE=$\frac{24}{5}$cm��
��֪����ABCD�������Խ���AC��BD���ֱ�Ϊ6cm��8cm����AE��BC��������ε����S=24cm2��AE=$\frac{24}{5}$cm��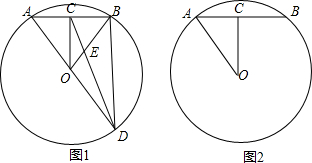
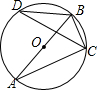 ��ͼ��AB�ǡ�O��ֱ������ABC=70�㣬���D�Ķ���Ϊ20�㣮
��ͼ��AB�ǡ�O��ֱ������ABC=70�㣬���D�Ķ���Ϊ20�㣮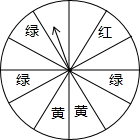 ij����Ϊ�������˿ͣ����г��ײ��Żݻ���ײ�ÿ��20Ԫ��ÿ����һ����ֱ�ӻ��10Ԫ�̈́������߲�����ϷӮ�ò̈́�����Ϸ�������£�������һ����������ת����ת�̣���ͼ��ת�̱�ƽ���ֳ�12�ݣ����˿�ÿ����һ���ײͣ��Ϳ��Ի��һ��ת��ת�̵Ļ��ᣬ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ���հ�������ô�˿;Ϳ��Էֱ���20Ԫ��15Ԫ��10Ԫ��5Ԫ�̈́����´ξͲ�ʱ���Դ����ֽ����ѣ�
ij����Ϊ�������˿ͣ����г��ײ��Żݻ���ײ�ÿ��20Ԫ��ÿ����һ����ֱ�ӻ��10Ԫ�̈́������߲�����ϷӮ�ò̈́�����Ϸ�������£�������һ����������ת����ת�̣���ͼ��ת�̱�ƽ���ֳ�12�ݣ����˿�ÿ����һ���ײͣ��Ϳ��Ի��һ��ת��ת�̵Ļ��ᣬ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ���հ�������ô�˿;Ϳ��Էֱ���20Ԫ��15Ԫ��10Ԫ��5Ԫ�̈́����´ξͲ�ʱ���Դ����ֽ����ѣ�