题目内容
12. 如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )
如果,正方形ABCD的边长为2cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q,若PQ=AE,则PD等于( )| A. | $\frac{2}{3}$cm或$\frac{2}{3}\sqrt{3}$cm | B. | $\frac{2}{3}\sqrt{3}$cm | C. | $\frac{4}{3}$cm或$\frac{2}{3}\sqrt{3}$cm | D. | $\frac{2}{3}$cm或$\frac{4}{3}$cm |
分析 根据题意画出图形,过P作PN⊥BC,交BC于点N,由ABCD为正方形,得到AD=DC=PN,在直角三角形ADE中,利用锐角三角函数定义求出DE的长,进而利用勾股定理求出AE的长,根据M为AE中点求出AM的长,利用HL得到三角形ADE与三角形PQN全等,利用全等三角形对应边,对应角相等得到DE=NQ,∠DAE=∠NPQ=30°,再由PN与DC平行,得到∠PFA=∠DEA=60°,进而得到PM垂直于AE,在直角三角形APM中,根据AM的长,利用锐角三角函数定义求出AP的长,进而得出DP的长.
解答 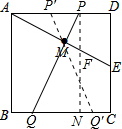 解:根据题意画出图形,过P作PN⊥BC,交BC于点N,
解:根据题意画出图形,过P作PN⊥BC,交BC于点N,
∵四边形ABCD为正方形,
∴AD=DC=PN,
在Rt△ADE中,∠DAE=30°,AD=2cm,
∴tan30°=$\frac{DE}{AD}$,即DE=$\frac{2\sqrt{3}}{3}$cm,
根据勾股定理得:AE=$\sqrt{{2}^{2}+(\frac{2\sqrt{3}}{3})^{2}}=\frac{4\sqrt{3}}{3}$cm,
∵M为AE的中点,
∴AM=$\frac{1}{2}$AE=$\frac{2\sqrt{3}}{3}$cm,
在Rt△ADE和Rt△PNQ中,
$\left\{\begin{array}{l}{AD=PN}\\{AE=PQ}\end{array}\right.$,
∴Rt△ADE≌Rt△PNQ(HL),
∴DE=NQ,∠DAE=∠NPQ=30°,
∵PN∥DC,
∴∠PFA=∠DEA=60°,
∴∠PMF=90°,即PM⊥AF,
在Rt△AMP中,∠MAP=30°,cos30°=$\frac{AM}{AP}$,
∴AP=$\frac{AM}{cos30°}=\frac{\frac{2\sqrt{3}}{3}}{\frac{\sqrt{3}}{2}}=\frac{4}{3}$cm,
所以PD=2-$\frac{4}{3}$=$\frac{2}{3}$或$\frac{4}{3}$.
故选D.
点评 此题考查了全等三角形的判定与性质,正方形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

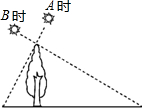 如图,小明在A时测得某树的影长为1m,B时又测得该树的影长为4米,若两次日照的光线互相垂直,树的高度为( )
如图,小明在A时测得某树的影长为1m,B时又测得该树的影长为4米,若两次日照的光线互相垂直,树的高度为( )| A. | 2m | B. | $\sqrt{3}$m | C. | $\sqrt{2}$m | D. | $\sqrt{5}$m |
| A. | 9.05×106 | B. | 0.905×106 | C. | 0.905×107 | D. | 9.05×107 |
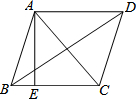 已知菱形ABCD的两条对角线AC,BD长分别为6cm、8cm,且AE⊥BC,这个菱形的面积S=24cm2,AE=$\frac{24}{5}$cm.
已知菱形ABCD的两条对角线AC,BD长分别为6cm、8cm,且AE⊥BC,这个菱形的面积S=24cm2,AE=$\frac{24}{5}$cm.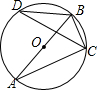 如图,AB是⊙O的直径,∠ABC=70°,则∠D的度数为20°.
如图,AB是⊙O的直径,∠ABC=70°,则∠D的度数为20°.