题目内容
 如图,四边形ABCD是平行四边形,点A,B,C在⊙O上,AD与⊙O相切,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,且∠PCB=2∠BAF.
如图,四边形ABCD是平行四边形,点A,B,C在⊙O上,AD与⊙O相切,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,且∠PCB=2∠BAF.(1)求证:直线PC是⊙O的切线;
(2)若AB=
| 10 |
考点:切线的判定,勾股定理,平行四边形的性质,相似三角形的判定与性质
专题:
分析:(1)首先连接OC,由AD与⊙O相切,可得FA⊥AD,四边形ABCD是平行四边形,可得AD∥BC,然后由垂径定理可证得F是
的中点,BE=CE,∠OEC=90°,又由∠PCB=2∠BAF,即可求得∠OCE+∠PCB=90°,继而证得直线PC是⊙O的切线;
(2)首先由勾股定理可求得AE的长,然后设⊙O的半径为r,则OC=OA=r,OE=3-r,则可求得半径长,易得△OCE∽△CPE,然后由相似三角形的对应边成比例,求得线段PC的长.
 |
| BC |
(2)首先由勾股定理可求得AE的长,然后设⊙O的半径为r,则OC=OA=r,OE=3-r,则可求得半径长,易得△OCE∽△CPE,然后由相似三角形的对应边成比例,求得线段PC的长.
解答: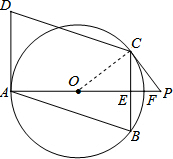 (1)证明:连接OC.
(1)证明:连接OC.
∵AD与⊙O相切于点A,
∴FA⊥AD.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴FA⊥BC.
∵FA经过圆心O,
∴F是
的中点,BE=CE,∠OEC=90°,
∴∠COF=2∠BAF.
∵∠PCB=2∠BAF,
∴∠PCB=∠COF.
∵∠OCE+∠COF=180°-∠OEC=90°,
∴∠OCE+∠PCB=90°.
∴OC⊥PC.
∵点C在⊙O上,
∴直线PC是⊙O的切线.
(2)解:∵四边形ABCD是平行四边形,
∴BC=AD=2.
∴BE=CE=1.
在Rt△ABE中,∠AEB=90°,AB=
,
∴AE=
=3.
设⊙O的半径为r,则OC=OA=r,OE=3-r.
在Rt△OCE中,∠OEC=90°,
∴OC2=OE2+CE2.
∴r2=(3-r)2+1.
解得r=
,
∵∠COE=∠PCE,∠OEC=∠CEP=90°.
∴△OCE∽△CPE,
∴
=
.
∴
=
.
∴CP=
.
 (1)证明:连接OC.
(1)证明:连接OC.∵AD与⊙O相切于点A,
∴FA⊥AD.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴FA⊥BC.
∵FA经过圆心O,
∴F是
 |
| BC |
∴∠COF=2∠BAF.
∵∠PCB=2∠BAF,
∴∠PCB=∠COF.
∵∠OCE+∠COF=180°-∠OEC=90°,
∴∠OCE+∠PCB=90°.
∴OC⊥PC.
∵点C在⊙O上,
∴直线PC是⊙O的切线.
(2)解:∵四边形ABCD是平行四边形,
∴BC=AD=2.
∴BE=CE=1.
在Rt△ABE中,∠AEB=90°,AB=
| 10 |
∴AE=
| AB2-BE2 |
设⊙O的半径为r,则OC=OA=r,OE=3-r.
在Rt△OCE中,∠OEC=90°,
∴OC2=OE2+CE2.
∴r2=(3-r)2+1.
解得r=
| 5 |
| 3 |
∵∠COE=∠PCE,∠OEC=∠CEP=90°.
∴△OCE∽△CPE,
∴
| OE |
| CE |
| OC |
| CP |
∴
3-
| ||
| 1 |
| ||
| CP |
∴CP=
| 5 |
| 4 |
点评:此题考查了切线的判定、平行四边形的性质、勾股定理以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
已知关于x的方程
+2=
有解,则k的取值范围是( )
| 1-x |
| x-2 |
| k |
| 2-x |
| A、k≠1 | B、k≠2 |
| C、k>1 | D、k≠-1 |
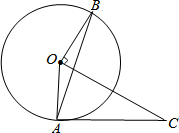 如图△AOC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于点B,垂足为点O,连接AB交OC于点D,∠CAD=∠CDA.
如图△AOC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于点B,垂足为点O,连接AB交OC于点D,∠CAD=∠CDA.(1)求证:AC是⊙O的切线;
(2)若OA=5,OD=1,求线段AC的长.
一个不透明的口袋内装有大小和形状相同的一个白球和两个红球,“从中任取一球,得到白球”这个事件是( )
| A、必然事件 | B、随机事件 |
| C、不可能事件 | D、以上都不正确 |
已知点P(x,y) 是第三象限内的一点,且x2=4,|y|=3,则P点的坐标是( )
| A、(-2,-3) |
| B、(2,3) |
| C、(-2,3) |
| D、(2,-3) |
 甲、乙两车从A地出发前往B地.在整个行程中,汽车离开A地的距离 y(km)与时间t(h)的对应关系如图所示,则乙车的平均速度为
甲、乙两车从A地出发前往B地.在整个行程中,汽车离开A地的距离 y(km)与时间t(h)的对应关系如图所示,则乙车的平均速度为