题目内容

甲、乙两车从A地出发前往B地．在整个行程中，汽车离开A地的距离 y（km）与时间t（h）的对应关系如图所示，则乙车的平均速度为
 
km/h；图中a的值为
 
km；在乙车行驶的过程中，当t=
 
h时，两车相距20km．
考点：一次函数的应用
专题：
分析：由速度=路程÷时间就可以乙的速度，由函数图象的数据求出两车相遇的时间就可以求出路程a的值，由追击问题的数量关系建立方程就可以求出两车相距20km时t的值．
解答：解：由题意，得
乙车的平均速度为：350÷（4.5-1）=100km/h，
甲车的速度为：350÷5=70km/h，
设乙出发x小时追上甲车，由题意，得
70（x+1）=100x，
解得：x=
7
3
，
∴a=
7
3
×100=
700
3
km．
当70t-100（t-1）=20时，
t=
8
3
．
当100（t-1）-70t=20时，
解得：t=4．
故答案为：100，
700
3
，
8
3
或4．
点评：本题考查了行程问题的追击问题的数量关系的运用，一次函数的图象的运用，解答时分析清楚函数图象的数据的含义是关键．
练习册系列答案
相关题目
-43÷（-32）-[(-
2
3
)3×（-32）+（-
11
3
）]．
已知：2+
2
3
=22×
2
3
，3+
3
8
=32×
3
8
，4+
4
15
=42×
4
15
，5+
5
24
=52×
5
24
，…若10+
b
a
=102×
b
a
，符合前面式子的规律，则（a-b）的值是
 
．
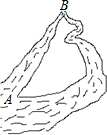如图，把原来弯曲的河道改直，A，B两地间的河道长度变短，这样做的道理是（　　）
A、两点确定一条直线
B、两点确定一条线段
C、两点之间，直线最短
D、两点之间，线段最短
若∠α=20°40′，则∠α的补角的大小为
 
．
为了了解九年级（2）班学生的视力情况，对全班同学进行调查，这种调查采用的方式是
 
．
将抛物线y=-2x2向右平移2个单位，得到的抛物线的解析式是
 
．
如图，四边形ABCD是平行四边形，点A，B，C在⊙O上，AD与⊙O相切，射线AO交BC于点E，交⊙O于点F．点P在射线AO上，且∠PCB=2∠BAF．
（1）求证：直线PC是⊙O的切线；
（2）若AB=
10
，AD=2，求线段PC的长．
二次函数y=-（x+1）2-2的最大值是（　　）
A、-2B、-1C、1D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网