题目内容
5.分解因式:(1)9a2-1
(2)3m2-24m+36
(3)(x2+y2)2-4x2y2.
分析 (1)直接利用平方差公式分解因式得出答案;
(2)首先提取公因式3,进而利用十字线乘法分解因式得出答案;
(3)首先利用平方差公式分解因式进而结合完全平方公式分解因式即可.
解答 解:(1)9a2-1=(3a+1)(3a-1);
(2)3m2-24m+36
=3(m2-8m+12)
=3(m-2)(m-6);
(3)(x2+y2)2-4x2y2
=(x2+y2-2xy)(x2+y2+2xy)
=(x+y)2(x-y)2.
点评 此题主要考查了提取公因式法以及公式法和十字相乘法分解因式,正确应用公式法分解因式是解题关键.

练习册系列答案
相关题目
18. 如图,在4×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
如图,在4×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
 如图,在4×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
如图,在4×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
10.下列图案中,既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.将抛物线y=2x2+1绕原点O旋转180°,则旋转后的抛物线的解析式为( )
| A. | y=-2x2 | B. | y=-2x2+1 | C. | y=2x2-1 | D. | y=-2x2-1 |
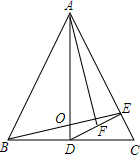 如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,DE⊥AC,垂足为E,且DF=EF,求证:AF⊥BE.
如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,DE⊥AC,垂足为E,且DF=EF,求证:AF⊥BE. 如图,F是平行四边形ABCD的边CD上的点,FD=2FC,连结AF并延长交BC于E,CE=2,则AD的长为( )
如图,F是平行四边形ABCD的边CD上的点,FD=2FC,连结AF并延长交BC于E,CE=2,则AD的长为( )