题目内容
13.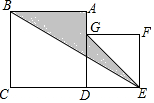 正方形ABCD与正方形DEFG如图所示摆放,正方形ABCD的边长为acm,正方形DEFG的边长为bcm.
正方形ABCD与正方形DEFG如图所示摆放,正方形ABCD的边长为acm,正方形DEFG的边长为bcm.(1)用含a,b的式子表示阴影部分的面积(温馨提示:a(a+b)=a2+ab)
(2)当a=6,b=4时,求阴影部分的面积.
分析 根据图形得结构可利用大图形的面积减去小图形的面积即可求出答案
解答 解:(1)两个正方形的面积为:a2+b2,Rt△BCE的面积为:$\frac{1}{2}$a(a+b),Rt△GFE的面积为:$\frac{1}{2}$b2,
∴阴影部分的面积为:a2+b2-$\frac{1}{2}$a(a+b)-$\frac{1}{2}$b2=a2+b2-$\frac{1}{2}$a2-$\frac{1}{2}$ab-$\frac{1}{2}$b2=$\frac{1}{2}$a2-$\frac{1}{2}$ab+$\frac{1}{2}$b2,
(2)当a=6,b=4时,
∴阴影部分的面积为:$\frac{1}{2}$×36-$\frac{1}{2}$×6×4+$\frac{1}{2}$×42=18-12+8=14
点评 本题考查列代数式求值,涉及化简代入求值,列代数式,整数运算等知识.

练习册系列答案
相关题目
1.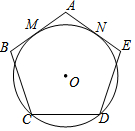 如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧MN的长度为( )
如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧MN的长度为( )
 如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧MN的长度为( )
如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧MN的长度为( )| A. | $\frac{1}{5}$π | B. | $\frac{2}{5}$π | C. | $\frac{\sqrt{3}}{5}$π | D. | $\frac{1}{3}$π |
2.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如表(单位:环):
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)已知甲六次成绩的方差S甲2=$\frac{2}{3}$,试计算乙六次测试成绩的方差;根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(2)已知甲六次成绩的方差S甲2=$\frac{2}{3}$,试计算乙六次测试成绩的方差;根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
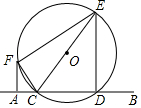 直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
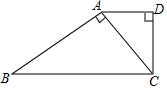 如图,已知直角梯形ABCD中,AD∥BC,∠D=90°,∠B=30°,CD=9$\sqrt{3}$,对角线CA⊥AB,求AD和BC的长度.
如图,已知直角梯形ABCD中,AD∥BC,∠D=90°,∠B=30°,CD=9$\sqrt{3}$,对角线CA⊥AB,求AD和BC的长度.