题目内容
4．已知在直角坐标系中，已知△ABC中，AB=AC，A、C的坐标分别为（0，-1）、（1，3），点B在x轴上，求点B的坐标．分析 先根据两点间的距离得出AC=$\sqrt{17}$，再根据AB=AC，点B在x轴上，得出点B的坐标即可．
解答 解：∵A、C的坐标分别为（0，-1）、（1，3），
∴AC=$\sqrt{{1}^{2}+（1+3）^{2}}=\sqrt{17}$，
∵AB=AC，
∴AB=$\sqrt{17}$，
∵点B在x轴上，
∴点B的坐标为（-4，0）或（4，0）．
点评 此题考查等腰三角形的性质，关键是根据两点之间的距离得出AC的值．
练习册系列答案
相关题目
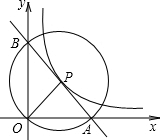如图，在平面直角坐标系中，O为坐标原点，P是反比例函数y=$\frac{k}{x}$（x＞0）的图象上任意一点，以P为圆心，PO为半径的圆与x轴、y轴分别交于点A、B．
如图，l1反映了某公司产品的销售收入与销售量之间的关系；l2反映了该公司产品的销售成本与销售量之间的关系，请根据图象提供的信息，求直线l1和直线l2对应的函数解析式．
如图，在?ABCD中，点E、F分别在AB，CD上，且AE=CF，DF=BF，求证：四边形DEBF为菱形．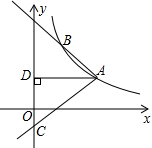
如图，反比例函数y=$\frac{k}{x}$（x＞0）的图象经过点A（2$\sqrt{3}$，1），射线AB与反比例函数的图象交于另一点B（1，a），射线AC与y轴交于点C，∠BAC=75°，AD⊥y轴，垂足为D．
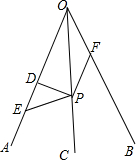如图，OC平分∠AOB，P为OC上一点，PD⊥OA于点D，∠PEO+∠PFO=180°，试求OE+OF与2OD的关系．
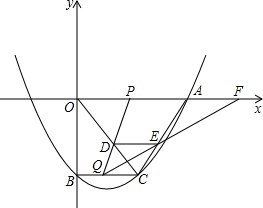如图，抛物线y=$\frac{1}{18}{x^2}-\frac{4}{9}$x-10与轴的一个交点为A，与y轴的交点为B．过点B作BC∥x轴，交抛物线于点C，连接AC．动点P、Q分别从0、C两点同时出发，动点P以每秒4个单位的速度沿OA向终点A移动，动点Q以每秒1个单位的速度沿CB向点B移动，当点P停止运动时，点Q也同时停止运动．线段PQ与OC的交点为D，过点D作DE∥x轴，交AC于点E，射线QE交X轴于点F．设点P、Q移动的时间为t（单位：秒）．