题目内容
16.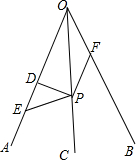 如图,OC平分∠AOB,P为OC上一点,PD⊥OA于点D,∠PEO+∠PFO=180°,试求OE+OF与2OD的关系.
如图,OC平分∠AOB,P为OC上一点,PD⊥OA于点D,∠PEO+∠PFO=180°,试求OE+OF与2OD的关系.
分析 过点P作PG⊥OB于G,先求出∠DEP=∠PFG,然后利用“角角边”证明△PDE和△PFG全等,根据全等三角形对应边相等可得DE=FG,再根据线段的和差解答即可.
解答 解:相等,理由如下:
过点P作PG⊥OB于G,如图: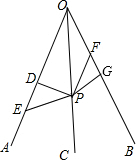
∵PG⊥OB,PD⊥OA,OC平分∠AOB,
∴PD=PG,
∵∠PEO+∠PFO=180°,∠PEO+∠PED=180°,
∴∠DEP=∠PFG,
在△PED与△PFG中,
$\left\{\begin{array}{l}{∠DEP=∠PFG}\\{∠EDP=∠BGP=90°}\\{PD=PG}\end{array}\right.$,
∴△PED≌△PFG(AAS),
同理可得△POD≌△POG,
∴OD=OG,DE=FG,
∴OE+OF=OF+OD+GF=OD+OG=2OD.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,到角的两边距离相等的点在角的平分线上的证明,全等三角形的判定与性质,熟记性质并理解证明方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
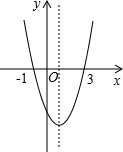 二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①bc<0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③4a-2b+c>0;④当x>0时,y随x值的增大而增大;⑤当y>0时,-1<x<3.其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①bc<0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③4a-2b+c>0;④当x>0时,y随x值的增大而增大;⑤当y>0时,-1<x<3.其中正确的个数是( )