题目内容
19．
如图，在?ABCD中，点E、F分别在AB，CD上，且AE=CF，DF=BF，求证：四边形DEBF为菱形．
分析 首先根据平行四边形的性质可得DC=AB，DC∥AB，再根据条件AE=CF可得DF=BE，然后再证明四边形DFBE是平行四边形，由条件DF=BF可得四边形DEBF为菱形．
解答 证明：∵四边形ABCD是平行四边形，
∴DC=AB，DC∥AB，
∵AE=CF，
∴AB-AE=DC-CF，
即DF=BE，
∴四边形DFBE是平行四边形，
∵DF=BF，
∴四边形DEBF为菱形．
点评 此题主要考查了菱形的判定，以及平行四边形的性质，关键是掌握一组邻边相等的平行四边形是菱形．
练习册系列答案
阅读快车系列答案
相关题目
如图，在平面直角坐标系中，⊙P的圆心坐标是（3，a）（a＞3），半径为3，函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{2}$，则a的值是3+$\sqrt{2}$．
8．
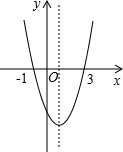二次函数y=ax2+bx+c的图象如图所示，给出下列说法：①bc＜0；②方程ax2+bx+c=0的根为x1=-1，x2=3；③4a-2b+c＞0；④当x＞0时，y随x值的增大而增大；⑤当y＞0时，-1＜x＜3．其中正确的个数是（ ）
二次函数y=ax2+bx+c的图象如图所示，给出下列说法：①bc＜0；②方程ax2+bx+c=0的根为x1=-1，x2=3；③4a-2b+c＞0；④当x＞0时，y随x值的增大而增大；⑤当y＞0时，-1＜x＜3．其中正确的个数是（ ）| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
9．下列是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{\frac{1}{x}+y=4}\\{x-y=1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+1=1}\\{y-z=2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{y=2x+5}\\{3x=-6}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{xy=1}\\{x+y=2}\end{array}\right.$ |