题目内容
12．袋中有三个小球，分别为1个红球和2个黄球，它们除颜色外完全相同．随机取出一个小球然后放回，再随机取出一个小球，则两次取出的小球颜色不相同的概率为$\frac{4}{9}$．分析 根据题意列表，再根据表格即可求得所有等可能的结果与两次取出的小球颜色相同的情况，然后根据概率公式求解．
解答 解：列表得：
| 红 | 黄 | 黄 | |
| 红 | （红，红） | （黄，红） | （黄，红） |
| 黄 | （黄，红） | （黄，黄） | （黄，黄） |
| 黄 | （黄，红） | （黄，黄） | （黄，黄） |
所以两次取出的小球颜色不相同的概率=$\frac{4}{9}$，
故答案为：$\frac{4}{9}$．
点评 此题考查了树状图法与列表法求概率．解题的关键是根据题意列表或画树状图，注意列表法与树状图法可以不重不漏的表示出所有等可能的结果．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
3．
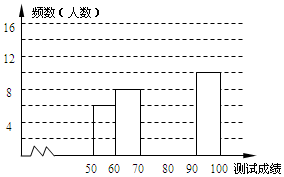“赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
请结合图表完成下列各题：
（1）①表中a的值为12； ②频数分布直方图补充完整；
（2）若测试成绩不低于80分为优秀，则本次测试的优秀率是44%．
（3）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小明与小强两名男同学能分在同一组的概率．
“赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：| 组别 | 成绩x分 | 频数（人数） |
| 第1组 | 50≤x＜60 | 6 |
| 第2组 | 60≤x＜70 | 8 |
| 第3组 | 70≤x＜80 | 14 |
| 第4组 | 80≤x＜90 | a |
| 第5组 | 90≤x＜100 | 10 |
（1）①表中a的值为12； ②频数分布直方图补充完整；
（2）若测试成绩不低于80分为优秀，则本次测试的优秀率是44%．
（3）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小明与小强两名男同学能分在同一组的概率．
20．
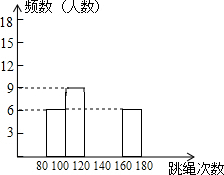某校为了了解九年级学生（共450人）的身体素质情况，体育老师对九（1）班的50位学生进行一分钟跳绳次数测试，以测试数据为样本，绘制了如下部分频数分布表和部分频数分布直方图．
请结合图表解答下列问题：
（1）表中的m=12；
（2）请把频数分布直方图补完整；
（3）这个样本数据的中位数落在第三组；
（4）若九年级学生一分钟跳绳次数（x）合格要求是x≥120，则估计九年级学生中一分钟跳绳成绩不合格的人数．
某校为了了解九年级学生（共450人）的身体素质情况，体育老师对九（1）班的50位学生进行一分钟跳绳次数测试，以测试数据为样本，绘制了如下部分频数分布表和部分频数分布直方图．| 组别 | 次数x | 频数（人数） |
| A | 80≤x＜100 | 6 |
| B | 100≤x＜120 | 8 |
| C | 120≤x＜140 | m |
| D | 140≤x＜160 | 18 |
| E | 160≤x＜180 | 6 |
（1）表中的m=12；
（2）请把频数分布直方图补完整；
（3）这个样本数据的中位数落在第三组；
（4）若九年级学生一分钟跳绳次数（x）合格要求是x≥120，则估计九年级学生中一分钟跳绳成绩不合格的人数．
1．下列运算错误的是（ ）
| A． | （x2）3=x6 | B． | x2•x3=x5 | C． | x2-2xy+y2=（x-y）2 | D． | 3x-2x=1 |
如图，将矩形纸片ABCD折叠，使点C与点A重合，折痕EF分别与AB、DC交于点E和点F．