题目内容
7．袋中有三个小球，分别为2个红球和3个黄球，它们除颜色外完全相同．随机取出一个小球然后不放回，再随机取出一个小球，则两次取出的小球颜色相同的概率为$\frac{2}{5}$．分析 根据题意画出树状图，再根据树状图即可求得所有等可能的结果与两次取出的小球颜色相同的情况，然后根据概率公式求解．
解答 解：画树状图如下：
由树状图可知，共有20种等可能结果，其中两次取出的小球颜色相同的有8种结果，
∴两次取出的小球颜色相同的概率为$\frac{8}{20}$=$\frac{2}{5}$，
故答案为：$\frac{2}{5}$．
点评 此题考查了树状图法与列表法求概率．解题的关键是根据题意列表或画树状图，注意列表法与树状图法可以不重不漏的表示出所有等可能的结果．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知等边三角形ABC，D是AB边上一点，作DE⊥AB交AC于点F，交BC延长线于点E，求证：CE=CF．
19．中国最大的水果公司“佳沃鑫荣懋”旗下子公司“欢乐果园”购进某种水果的成本为20元/kg，经过市场调研发现，这种水果在未来48天的销售单价p（元/kg）与时间t（天）之间的函数关系式为P=$\left\{\begin{array}{l}{\frac{1}{4}t+30（1≤t≤24，t为整数）}\\{-\frac{1}{2}t+48（25≤t≤48，t为整数）}\end{array}\right.$，且其日销售量y（kg）与时间t（天）的关系如表：
（1）已知y与t之间的变化规律符合一次函数关系，试求在第30天的日销售量是多少？
（2）问哪一天的销售利润最大？最大日销售利润为多少？
（3）在实际销售前24天中，子公司决定每销售1kg水果就捐赠n元利润（n＜9）给“精准扶贫”对象．现发现：在前24天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求n的取值范围．
| 时间t（天） | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y（kg） | 118 | 114 | 108 | 100 | 80 | 40 | … |
（2）问哪一天的销售利润最大？最大日销售利润为多少？
（3）在实际销售前24天中，子公司决定每销售1kg水果就捐赠n元利润（n＜9）给“精准扶贫”对象．现发现：在前24天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求n的取值范围．
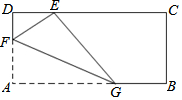如图，矩形纸片ABCD中，AD=1，将纸片折叠，使顶点A与CD边上的点E重合，折痕FG分别与AD、AB交于点F、G，若DE=$\frac{{\sqrt{3}}}{3}$，则EF的长为$\frac{2}{3}$．