题目内容
学校为了了解初三年级学生体育跳绳的训练情况,从初三年级各班随机抽取了50名学生进行了60秒跳绳的测试,并将这50名学生的测试成绩(即60秒跳绳的个数)从低到高分成六段记为第一到六组,最后整理成下面的频数分布直方图:请根据直方图中样本数据提供的信息解答下列问题.
(1)跳绳次数的中位数落在哪一组?由样本数据的中位数你能推断出学校初三年级学生关于60秒跳绳成绩的一个什么结论?
(2)若用各组数据的组中值(各小组的两个端点的数的平均数)代表各组的实际数据,求这50名学生的60秒跳绳的平均成绩(结果保留整数);
(3)若从成绩落在第一和第六组的学生中随机抽取2名学生,用列举法求抽取的2名学生恰好在同一组的概率.

(1)跳绳次数的中位数落在哪一组?由样本数据的中位数你能推断出学校初三年级学生关于60秒跳绳成绩的一个什么结论?
(2)若用各组数据的组中值(各小组的两个端点的数的平均数)代表各组的实际数据,求这50名学生的60秒跳绳的平均成绩(结果保留整数);
(3)若从成绩落在第一和第六组的学生中随机抽取2名学生,用列举法求抽取的2名学生恰好在同一组的概率.

考点:频数(率)分布直方图,中位数,列表法与树状图法
专题:图表型
分析:(1)根据中位数的定义先把这组数据从小到大排列,找出中间两个数的平均数,再根据中位数落在第四组估计出初三学生60秒跳绳再120个以上的人数达到一半以上;
(2)根据平均数的计算公式进行计算即可;
(3)先把第一组的两名学生用A、B表示,第六组的三名学生用1,2,3表示,得出所有出现的情况,再根据概率公式进行计算即可.
(2)根据平均数的计算公式进行计算即可;
(3)先把第一组的两名学生用A、B表示,第六组的三名学生用1,2,3表示,得出所有出现的情况,再根据概率公式进行计算即可.
解答:解:(1)∵共有50个数,中位数是第25、26个数的平均数,
∴跳绳次数的中位数落在第四组;
∴可以估计初三学生60秒跳绳再120个以上的人数达到一半以上;
(2)根据题意得:
(2×70+10×90+12×110+13×130+10×150+3×170)÷50≈121(个),
答:这50名学生的60秒跳绳的平均成绩是121个;
(3)记第一组的两名学生为A、B,第六组的三名学生为1,2,3,
则从这5名学生中抽取两名学生有以下10种情况:
AB,A1,A2,A3,B1,B2,B3,12,13,23,
则抽取的2名学生恰好在同一组的概率是:
=
;
∴跳绳次数的中位数落在第四组;
∴可以估计初三学生60秒跳绳再120个以上的人数达到一半以上;
(2)根据题意得:
(2×70+10×90+12×110+13×130+10×150+3×170)÷50≈121(个),
答:这50名学生的60秒跳绳的平均成绩是121个;
(3)记第一组的两名学生为A、B,第六组的三名学生为1,2,3,
则从这5名学生中抽取两名学生有以下10种情况:
AB,A1,A2,A3,B1,B2,B3,12,13,23,
则抽取的2名学生恰好在同一组的概率是:
| 4 |
| 10 |
| 2 |
| 5 |
点评:此题考查了频数(率)分布直方图,用到的知识点是中位数、平均数、概率公式,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表: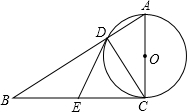 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.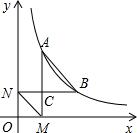 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数. 一只自由飞行的小鸟,将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在阴影方格地面上的概率是
一只自由飞行的小鸟,将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在阴影方格地面上的概率是