题目内容
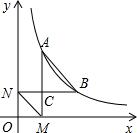 如图,已知反比例函数y=
如图,已知反比例函数y=| k |
| x |
(1)写出反比例函数解析式;
(2)求证:△ACB∽△NOM;
(3)若△ACB与△NOM的相似比为2,求出B点的坐标及AB所在直线的解析式.
考点:反比例函数综合题
专题:数形结合
分析:(1)把A点坐标代入y=
可得k的值,进而得到函数解析式;
(2)根据A、B两点坐标可得AC=4-n,BC=m-1,ON=n,OM=1,则
=
,再根据反比例函数解析式可得
=m,则
=m-1,而
=
,可得
=
,再由∠ACB=∠NOM=90°,可得△ACB∽△NOM;
(3)根据△ACB与△NOM的相似比为2可得m-1=2,进而得到m的值,然后可得B点坐标,再利用待定系数法求出AB的解析式即可.
| k |
| x |
(2)根据A、B两点坐标可得AC=4-n,BC=m-1,ON=n,OM=1,则
| AC |
| NO |
| 4-n |
| n |
| 4 |
| n |
| AC |
| ON |
| BC |
| MO |
| m-1 |
| 1 |
| AC |
| NO |
| BC |
| MO |
(3)根据△ACB与△NOM的相似比为2可得m-1=2,进而得到m的值,然后可得B点坐标,再利用待定系数法求出AB的解析式即可.
解答:解:(1)∵y=
(x>0,k是常数)的图象经过点A(1,4),
∴k=4,
∴反比例函数解析式为y=
;
(2)∵点A(1,4),点B(m,n),
∴AC=4-n,BC=m-1,ON=n,OM=1,
∴
=
=
-1,
∵B(m,n)在y=
上,
∴
=m,
∴
=m-1,而
=
,
∴
=
,
∵∠ACB=∠NOM=90°,
∴△ACB∽△NOM;
(3)∵△ACB与△NOM的相似比为2,
∴m-1=2,
m=3,
∴B(3,
),
设AB所在直线解析式为y=kx+b,
∴
,
解得
,
∴解析式为y=-
x+
.
| k |
| x |
∴k=4,
∴反比例函数解析式为y=
| 4 |
| x |
(2)∵点A(1,4),点B(m,n),
∴AC=4-n,BC=m-1,ON=n,OM=1,
∴
| AC |
| NO |
| 4-n |
| n |
| 4 |
| n |
∵B(m,n)在y=
| 4 |
| x |
∴
| 4 |
| n |
∴
| AC |
| ON |
| BC |
| MO |
| m-1 |
| 1 |
∴
| AC |
| NO |
| BC |
| MO |
∵∠ACB=∠NOM=90°,
∴△ACB∽△NOM;
(3)∵△ACB与△NOM的相似比为2,
∴m-1=2,
m=3,
∴B(3,
| 4 |
| 3 |
设AB所在直线解析式为y=kx+b,
∴
|
解得
|
∴解析式为y=-
| 4 |
| 3 |
| 16 |
| 3 |
点评:此题主要考查了反比例函数的综合应用,关键是掌握凡是函数图象经过的点,必然能使函数解析式左右相等.

练习册系列答案
相关题目
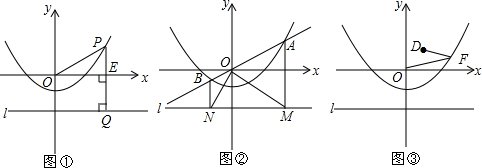
 如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=
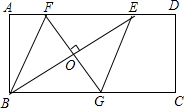
如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE= 如图,?ABCD的对角线AC、BD相交于点O,EF过点O且与AB,CD分别相交于点E、F,求证:△AOE≌△COF.
如图,?ABCD的对角线AC、BD相交于点O,EF过点O且与AB,CD分别相交于点E、F,求证:△AOE≌△COF.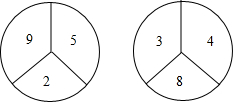 有两个构造完全相同(除所标数字外)的转盘A、B,游戏规定,转动两个转盘各一次,指向大的数字获胜.现由你和小明各选择一个转盘游戏,你会选择哪一个,为什么?
有两个构造完全相同(除所标数字外)的转盘A、B,游戏规定,转动两个转盘各一次,指向大的数字获胜.现由你和小明各选择一个转盘游戏,你会选择哪一个,为什么?
 如图,已知点A、B、C在⊙O上,CD⊥OB于D,AB=2OD,若∠C=40°,则∠B=
如图,已知点A、B、C在⊙O上,CD⊥OB于D,AB=2OD,若∠C=40°,则∠B= 如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生700人,则据此估计步行的有
如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生700人,则据此估计步行的有 如图,已知:a∥b,∠3=137°,则∠2=
如图,已知:a∥b,∠3=137°,则∠2=