题目内容
 如图,在△ABC中,BC=4,AC=13,AB=15,求S△ABC.
如图,在△ABC中,BC=4,AC=13,AB=15,求S△ABC.考点:勾股定理
专题:
分析:如图,作BC边上的高,设出AD、CD的长,运用勾股定理列出关于线段AD的方程,求出AD的长,问题即可解决.
解答: 解:如图,过点A作AD⊥BC于点D;
解:如图,过点A作AD⊥BC于点D;
设AD=λ,CD=μ;由勾股定理得:
,
由②-①得:8μ=40,
∴μ=5,代入②并解得λ=12,
∴S△ABC=
×4×12=24.
 解:如图,过点A作AD⊥BC于点D;
解:如图,过点A作AD⊥BC于点D;设AD=λ,CD=μ;由勾股定理得:
|
由②-①得:8μ=40,
∴μ=5,代入②并解得λ=12,
∴S△ABC=
| 1 |
| 2 |
点评:该题主要考查了勾股定理在几何计算、化简、求值等方面的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、计算、推理或解答.

练习册系列答案
相关题目
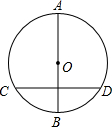 如图,在⊙O中AB为直径,CD为非直径的弦,(1)AB⊥CD;(2)AB平分CD;(3)AB平分CD所对的两条弧.若以(1)、(2)、(3)中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为( )
如图,在⊙O中AB为直径,CD为非直径的弦,(1)AB⊥CD;(2)AB平分CD;(3)AB平分CD所对的两条弧.若以(1)、(2)、(3)中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为( ) 如图,⊙O与抛物线y=
如图,⊙O与抛物线y=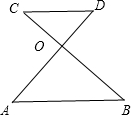 如图,OA=9,DA=12,BC=6,且
如图,OA=9,DA=12,BC=6,且 如图,在一个矩形纸片ABCD剪上减去一个正方形ABEF,所余下的矩形ECDF于原矩形ABCD相似,那么原矩形中较长的边BC与较短的边AB的比是多少?
如图,在一个矩形纸片ABCD剪上减去一个正方形ABEF,所余下的矩形ECDF于原矩形ABCD相似,那么原矩形中较长的边BC与较短的边AB的比是多少?