题目内容
20.如果关于x、y的方程组$\left\{\begin{array}{l}{x+2y=6+k}\\{2x-y=9-2k}\end{array}\right.$的解满足3x+y=5,则k的值=10.分析 首先解方程组,利用k表示出x、y的值,然后代入3x+y=5,即可得到一个关于k的方程,求得k的值.
解答 解:$\left\{\begin{array}{l}{x+2y=6+k…①}\\{2x-y=9-2k…②}\end{array}\right.$,
①+2×②得:5x=24+5k,
则x=$\frac{24+5k}{5}$,
①×2-②得:5y=3+4k,
解得:y=$\frac{3+4k}{5}$,
则$\frac{3(24+5k)}{5}$+$\frac{3+5k}{5}$=5,
解得:k=10.
故答案是:10.
点评 此题主要考查了二元一次方程组解的定义.以及解二元一次方程组的基本方法.正确解关于x、y的方程组是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.若实数a,b(a≠b)分别满足方程a2-7a+2=0,b2-7b+2=0,则$\frac{b}{a}$$+\frac{a}{b}$的值为( )
| A. | $\frac{45}{2}$ | B. | $\frac{49}{2}$ | C. | $\frac{45}{2}$或2 | D. | $\frac{49}{2}$或2 |
8.下列方程是一元二次方程的是( )
| A. | x2+2y=1 | B. | x3-2x=3 | C. | x2+$\frac{1}{{x}^{2}}$=5 | D. | x2=0 |
15.将方程组$\left\{\begin{array}{l}{2x-3y=9}\\{2x+4y=-1}\end{array}\right.$ 中的x消去后得到的方程是( )
| A. | y=8 | B. | 7y=10 | C. | -7y=8 | D. | -7y=10 |
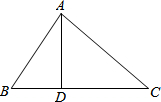 如图,在△ABC中,D是BC边上一点,AB=13,AD=12,BD=5,CD=9,求AC的长.
如图,在△ABC中,D是BC边上一点,AB=13,AD=12,BD=5,CD=9,求AC的长. 反比例函数y=$\frac{k+1}{x}$的图象如图所示,给出以下结论:
反比例函数y=$\frac{k+1}{x}$的图象如图所示,给出以下结论: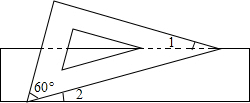 如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=15°,那么∠2的度数是15°.
如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=15°,那么∠2的度数是15°.