题目内容
11.(1)计算:|$\sqrt{2}$-1|-$\sqrt{8}$+2sin45°+($\frac{1}{2}$)-2;(2)解不等式组:$\left\{\begin{array}{l}{2x-7<3(x-1)①}\\{\frac{4}{3}x+3≤1-\frac{2}{3}x②}\end{array}\right.$.
分析 (1)原式利用二次根式性质,特殊角的三角函数值,以及负整数指数幂法则计算即可得到结果.
(2)分别求得两个不等式的解集,然后取其公共部分即可.
解答 解:(1)原式=$\sqrt{2}$-1-2$\sqrt{2}$+2×$\frac{\sqrt{2}}{2}$+4
=$\sqrt{2}$-1-2$\sqrt{2}$+$\sqrt{2}$+4
=3;
(2)$\left\{\begin{array}{l}{2x-7<3(x-1)①}\\{\frac{4}{3}x+3≤1-\frac{2}{3}x②}\end{array}\right.$,
①可化简为2x-7<3x-3,
-x<4,
x>-4,
②可化简为2x≤1-3,则x≤-1.
不等式的解集是-4<x≤-1.
点评 本题考查了解一元一次不等式组,实数的运算,负整数指数幂以及特殊角的三角函数值.熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.下列调查中,最适合采用全面调查(普查)方式的是( )
| A. | 对重庆市初中学生每天阅读时间的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对某批次手机的防水功能的调查 | |
| D. | 对某校九年级3班学生肺活量情况的调查 |
6.下列计算正确的是( )
| A. | a5+a5=a10 | B. | a7÷a=a6 | C. | a3•a2=a6 | D. | (-a3)2=-a6 |
3. 如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( )
如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( )
 如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( )
如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( )| A. | x>2 | B. | x<2 | C. | x>-1 | D. | x<-1 |
20.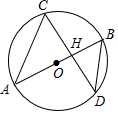 如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB=$\frac{4}{5}$,BD=5,则OH的长度为( )
如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB=$\frac{4}{5}$,BD=5,则OH的长度为( )
 如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB=$\frac{4}{5}$,BD=5,则OH的长度为( )
如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB=$\frac{4}{5}$,BD=5,则OH的长度为( )| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{7}{6}$ |
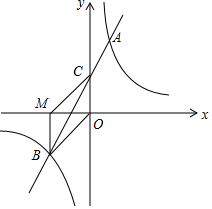 如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2$\sqrt{2}$,点A的纵坐标为4.
如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2$\sqrt{2}$,点A的纵坐标为4.
