题目内容
19.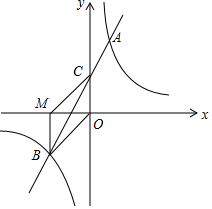 如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2$\sqrt{2}$,点A的纵坐标为4.
如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2$\sqrt{2}$,点A的纵坐标为4.(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.
分析 (1)根据题意可以求得点B的坐标,从而可以求得反比例函数的解析式,进而求得点A的坐标,从而可以求得一次函数的解析式;
(2)根据(1)中的函数解析式可以求得点C,点M、点B、点O的坐标,从而可以求得四边形MBOC的面积.
解答 解:(1)由题意可得,
BM=OM,OB=2$\sqrt{2}$,
∴BM=OM=2,
∴点B的坐标为(-2,-2),
设反比例函数的解析式为y=$\frac{k}{x}$,
则-2=$\frac{k}{-2}$,得k=4,
∴反比例函数的解析式为y=$\frac{4}{x}$,
∵点A的纵坐标是4,
∴4=$\frac{4}{x}$,得x=1,
∴点A的坐标为(1,4),
∵一次函数y=mx+n(m≠0)的图象过点A(1,4)、点B(-2,-2),
∴$\left\{\begin{array}{l}{m+n=4}\\{-2m+n=-2}\end{array}\right.$,得$\left\{\begin{array}{l}{m=2}\\{n=2}\end{array}\right.$,
即一次函数的解析式为y=2x+2;
(2)∵y=2x+2与y轴交与点C,
∴点C的坐标为(0,2),
∵点B(-2,-2),点M(-2,0),点O(0,0),
∴OM=2,OC=2,MB=2,
∴四边形MBOC的面积是:$\frac{OM•OC}{2}+\frac{OM•MB}{2}$=$\frac{2×2}{2}+\frac{2×2}{2}$=4.
点评 本题考查反比例函数与一次函数的交点问题,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质和反比例函数的性质解答.

练习册系列答案
相关题目
9.380亿用科学记数法表示为( )
| A. | 38×109 | B. | 0.38×1013 | C. | 3.8×1011 | D. | 3.8×1010 |
10.将分别标有“孔”“孟”“之”“乡”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀,随机摸出一球,不放回;再随机摸出一球,两次摸出的球上的汉字组成“孔孟”的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
7. 如图,矩形ABCD的边AB=1,BE平分∠ABC,交AD于点E,若点E是AD的中点,以点B为圆心,BE长为半径画弧,交BC于点F,则图中阴影部分的面积是( )
如图,矩形ABCD的边AB=1,BE平分∠ABC,交AD于点E,若点E是AD的中点,以点B为圆心,BE长为半径画弧,交BC于点F,则图中阴影部分的面积是( )
 如图,矩形ABCD的边AB=1,BE平分∠ABC,交AD于点E,若点E是AD的中点,以点B为圆心,BE长为半径画弧,交BC于点F,则图中阴影部分的面积是( )
如图,矩形ABCD的边AB=1,BE平分∠ABC,交AD于点E,若点E是AD的中点,以点B为圆心,BE长为半径画弧,交BC于点F,则图中阴影部分的面积是( )| A. | $2-\frac{π}{4}$ | B. | $\frac{3}{2}-\frac{π}{4}$ | C. | $2-\frac{π}{8}$ | D. | $\frac{3}{2}-\frac{π}{8}$ |
4.总投资647亿元的西成高铁预计2017年11月竣工,届时成都到西安只需3小时,上午游武侯区,晚上看大雁塔将成为现实,用科学记数法表示647亿元为( )
| A. | 647×108 | B. | 6.47×109 | C. | 6.47×1010 | D. | 6.47×1011 |
9.计算a5÷a3结果正确的是( )
| A. | a | B. | a2 | C. | a3 | D. | a4 |
 某班体育委员对本班学生一周锻炼时间(单位:小时)进行了统计,绘制了如图所示的折线统计图,则该班这些学生一周锻炼时间的中位数是11小时.
某班体育委员对本班学生一周锻炼时间(单位:小时)进行了统计,绘制了如图所示的折线统计图,则该班这些学生一周锻炼时间的中位数是11小时.