题目内容
20.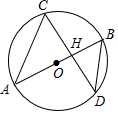 如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB=$\frac{4}{5}$,BD=5,则OH的长度为( )
如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB=$\frac{4}{5}$,BD=5,则OH的长度为( )| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{7}{6}$ |
分析 连接OD,由垂径定理得出AB⊥CD,由三角函数求出DH=4,由勾股定理得出BH=$\sqrt{B{D}^{2}-D{H}^{2}}$=3,设OH=x,则OD=OB=x+3,在Rt△ODH中,由勾股定理得出方程,解方程即可.
解答 解:连接OD,如图所示:
∵AB是⊙O的直径,且经过弦CD的中点H,
∴AB⊥CD,
∴∠OHD=∠BHD=90°,
∵cos∠CDB=$\frac{DH}{BD}$=$\frac{4}{5}$,BD=5,
∴DH=4,
∴BH=$\sqrt{B{D}^{2}-D{H}^{2}}$=3,
设OH=x,则OD=OB=x+3,
在Rt△ODH中,由勾股定理得:x2+42=(x+3)2,
解得:x=$\frac{7}{6}$,
∴OH=$\frac{7}{6}$;
故选:D.
点评 此题考查了垂径定理、勾股定理以及三角函数.此题难度不大,注意数形结合思想的应用.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
10.将分别标有“孔”“孟”“之”“乡”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀,随机摸出一球,不放回;再随机摸出一球,两次摸出的球上的汉字组成“孔孟”的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
15.2的相反数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
12.PM2.5是指大气中直径小于或等于2.5μm(1μm=0.000001m)的颗粒物,也称为可入肺颗粒物,它们含有一定量的有毒、有害物质,对人体健康和大气环境质量有很大影响.2.3μm用科学记数法可表示为( )
| A. | 23×10-5m | B. | 2.3×10-5m | C. | 2.3×10-6m | D. | 0.23×10-7m |
9.计算a5÷a3结果正确的是( )
| A. | a | B. | a2 | C. | a3 | D. | a4 |
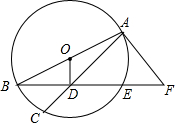 如图,AB是⊙O的直径,点E为弧AC的中点,AC、BE交于点D过A的切线交BE的延长线于F.
如图,AB是⊙O的直径,点E为弧AC的中点,AC、BE交于点D过A的切线交BE的延长线于F.