题目内容
8.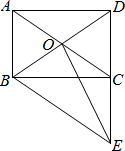 如图,矩形ABCD的对角线AC、BD相交于点O,过点B作BE∥AC,交DC的延长线于点E.
如图,矩形ABCD的对角线AC、BD相交于点O,过点B作BE∥AC,交DC的延长线于点E.(1)求证:△BDC≌△BEC;
(2)若BE=10,CE=6,连接OE,求OE的值.
分析 (1)根据矩形的性质得出AB=CD,AB∥DC,∠BCD=∠BCE=90°,求出四边形ABEC为平行四边形,求出DC=EC,根据SAS推出全等即可;
(2)过点O作OF⊥CD于点F,根据平行四边形的性质得出AC=BE,求出OF和EF的长,最后根据勾股定理求出EF即可.
解答 (1)证明:∵四边形ABCD为矩形,
∴AB=CD,AB∥DC,∠BCD=∠BCE=90°,
∵AC∥BE,
∴四边形ABEC为平行四边形,
∴AB=CE,
∴DC=EC,
在△BCD和△BCE中,
$\left\{\begin{array}{l}{BC=BC}\\{∠BCD=∠BCE}\\{DC=EC}\end{array}\right.$
∴△BCD≌△BCE;
(2)解:过点O作OF⊥CD于点F,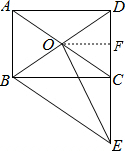
∵由(1)知:四边形ABEC为平行四边形,
∴AC=BE,
∴BE=BD=10,
∵△BCD≌△BCE,
∴CD=CE=6,
∵四边形ABCD是矩形,
∴DO=OB,∠BCD=90°,
∵OF⊥CD,
∴OF∥BC,
∴CF=DF=$\frac{1}{2}$CD=3,
∴EF=6+3=9,
在Rt△BCE中,由勾股定理可得BC=8,
∵OB=OD,
∴OF为△BCD的中位线,
∴OF=$\frac{1}{2}$BC=4.
∴在Rt△OEF中,由勾股定理可得OE=$\sqrt{O{F}^{2}+E{F}^{2}}$=$\sqrt{{4}^{2}+{9}^{2}}$=$\sqrt{97}$.
点评 本题考查了勾股定理,全等三角形的性质和判定,矩形的性质,平行四边形的性质和判定的应用,能综合运用知识点进行推理是解此题的关键,题目综合性比较强,难度偏大.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
18.用四舍五入法对3.8963取近似数,精确到0.01,得到的正确结果是( )
| A. | 3.89 | B. | 3.9 | C. | 3.90 | D. | 3.896 |
19.在下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.一组数据:3,4,5,6,6,的平均数、众数、中位数分别是( )
| A. | 4.8,6,6 | B. | 5,5,5 | C. | 4.8,6,5 | D. | 5,6,6 |
 在学习三视图时,老师在讲台上用四盒粉笔盒摆放出如图形状的几何体,那么该几何体的左视图正确的是( )
在学习三视图时,老师在讲台上用四盒粉笔盒摆放出如图形状的几何体,那么该几何体的左视图正确的是( )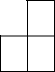


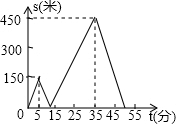 甲、乙两人匀速行走从同一地点到距离1500米处的图书馆,甲出发5分钟后,乙出发并沿同一路线行走,乙的速度是甲的速度的$\frac{5}{3}$.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示,下列说法
甲、乙两人匀速行走从同一地点到距离1500米处的图书馆,甲出发5分钟后,乙出发并沿同一路线行走,乙的速度是甲的速度的$\frac{5}{3}$.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示,下列说法 如图,A(2,1),B(1,-1),以O为位似中心,按比例尺1:2,把△AOB放大,则点A的对应点A′的坐标为(4,2)或(-4,-2).
如图,A(2,1),B(1,-1),以O为位似中心,按比例尺1:2,把△AOB放大,则点A的对应点A′的坐标为(4,2)或(-4,-2).