题目内容
13．
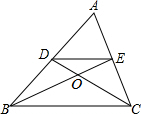如图，在△ABC中，两条中线BE，CD相交于点O，则S△DOE：S△DCE=1：3．
分析 直接根据三角形重心的性质即可得出结论．
解答 解：∵在△ABC中，两条中线BE，CD相交于点O，
∴点O是△ABC的重心，
∴OD：CD=1：3，
∴S△DOE：S△DCE=1：3．
故答案为：1：3．
点评 本题考查的是三角形的重心，熟知三角形的重心到顶点的距离与重心到对边中点的距离之比为2：1是解答此题的关键．
练习册系列答案
相关题目
3．下列四个数中，最小的正数是（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
4．
如图，已知∠1=60°，如果CD∥BE，那么∠B的度数为（ ）
如图，已知∠1=60°，如果CD∥BE，那么∠B的度数为（ ）| A． | 70° | B． | 100° | C． | 110° | D． | 120° |
如图，在△ABC中，∠B=60°，AB：AC=5：7，其内切圆⊙O与BC、AC、AB分别切于点D、E、F，且⊙O的面积为12π，求△ABC的三边长．
8．已知一元二次方程x2+bx-6=0有一个根为2，则另一根为（ ）
| A． | 2 | B． | -3 | C． | 4 | D． | 3 |
18．用四舍五入法对3.8963取近似数，精确到0.01，得到的正确结果是（ ）
| A． | 3.89 | B． | 3.9 | C． | 3.90 | D． | 3.896 |
5．已知反比例函数y=$\frac{k}{x}$（k≠0），当自变量x满足$\frac{1}{2}$≤x≤2时，对应的函数值y满足$\frac{1}{4}$≤y≤1，则k的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | 2 | D． | 4 |
小红在观察由一些相同小立方块搭成的几何体时，发现它的主视图、左视图、俯视图依次为如图所示的图形，若每个小正方形的面积为1，则该几何体的表面积为（ ）