题目内容
5.若a+b=2,则代数式a2-b2+4b=4.分析 先根据平方差公式不想,代入后合并同类项,再变形,代入求出即可.
解答 解:∵a+b=2,
∴a2-b2+4b
=(a+b)(a-b)+4b
=2(a-b)+4b
=2a+2b=2(a+b)
=2×2
=4,
故答案为:4.
点评 本题考查了平方差公式,能熟记平方差公式的内容是解此题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
2.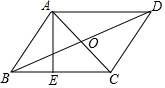 如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=$\sqrt{3}$,AC=2,BD=4,则AE的长为( )
如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=$\sqrt{3}$,AC=2,BD=4,则AE的长为( )
 如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=$\sqrt{3}$,AC=2,BD=4,则AE的长为( )
如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=$\sqrt{3}$,AC=2,BD=4,则AE的长为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{21}}{7}$ | D. | $\frac{2\sqrt{21}}{7}$ |
13.设A、B都是关于x的5次多项式,则下列说法正确的是( )
| A. | A+B是关于x的5次多项式 | B. | A-B是关于x的4次多项式 | ||
| C. | AB是关于x的10次多项式 | D. | $\frac{A}{B}$是与x无关的常数 |
17.下列计算结果为x5的是( )
| A. | x3+x2 | B. | x6÷x | C. | (x2)3 | D. | x7-x2 |
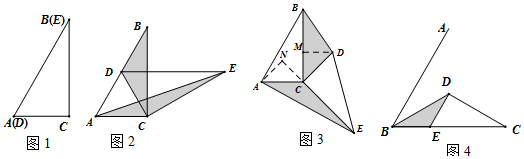
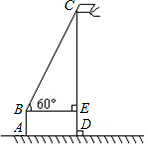 小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
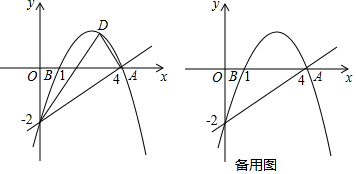
小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)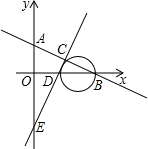 已知直线y=-$\frac{1}{2}$x+1与x轴、y轴分别交于B点、A点,直线y=2x-2与x轴、y轴分别交于D点、E点,两条直线交于点C;
已知直线y=-$\frac{1}{2}$x+1与x轴、y轴分别交于B点、A点,直线y=2x-2与x轴、y轴分别交于D点、E点,两条直线交于点C;