题目内容
2.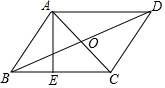 如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=$\sqrt{3}$,AC=2,BD=4,则AE的长为( )
如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=$\sqrt{3}$,AC=2,BD=4,则AE的长为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{21}}{7}$ | D. | $\frac{2\sqrt{21}}{7}$ |
分析 由勾股定理的逆定理可判定△BAO是直角三角形,所以平行四边形ABCD的面积即可求出.
解答 解:∵AC=2,BD=4,四边形ABCD是平行四边形,
∴AO=$\frac{1}{2}$AC=1,BO=$\frac{1}{2}$BD=2,
∵AB=$\sqrt{3}$,
∴AB2+AO2=BO2,
∴∠BAC=90°,
∵在Rt△BAC中,BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{2}^{2}}$=$\sqrt{7}$
S△BAC=$\frac{1}{2}$×AB×AC=$\frac{1}{2}$×BC×AE,
∴$\sqrt{3}$×2=$\sqrt{7}$AE,
∴AE=$\frac{2\sqrt{21}}{7}$,
故选D.
点评 本题考查了勾股定理的逆定理和平行四边形的性质,能得出△BAC是直角三角形是解此题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
12.在实数0,-π,$\sqrt{3}$,-4中,最小的数是( )
| A. | 0 | B. | $\sqrt{3}$ | C. | -4 | D. | -π |
13.用棋子摆出下列一组图形:

按照这种规律摆下去,第n个图形用的棋子个数为( )

按照这种规律摆下去,第n个图形用的棋子个数为( )
| A. | 3n | B. | 6n | C. | 3n+6 | D. | 3n+3 |
17.下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.下面的几何体中,主视图为圆的是( )
| A. |  | B. |  | C. |  | D. |  |
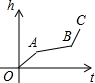 均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( )
均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( )