题目内容
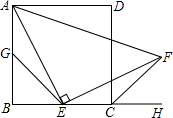 如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.(1)证明:△AGE≌△ECF;
(2)连接GD,DF.判断四边形GEFD的形状,并说明理由.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)G、E分别为AB、BC的中点,由正方形的性质可知AG=EC,△BEG为等腰直角三角形,则∠AGE=180°-45°=135°,而∠ECF=90°+45°=135°,得∠AGE=∠ECF,再利用互余关系,得∠GAE=90°-∠AEB=∠CEF,ASA可证△AGE≌△ECF;
(2)过点F作FM⊥BH于M,过F作FN⊥DC于N,首先证明△AGD≌△ABE,所以GD=AE,再证明△AGD≌△EFM,所以GD=EF,再通过证明△DFN≌△BGE可得到DF=GE,所以四边形GEFD是平行四边形.
(2)过点F作FM⊥BH于M,过F作FN⊥DC于N,首先证明△AGD≌△ABE,所以GD=AE,再证明△AGD≌△EFM,所以GD=EF,再通过证明△DFN≌△BGE可得到DF=GE,所以四边形GEFD是平行四边形.
解答:证明:∵正方形ABCD,点G,E为边AB、BC中点,
∴AG=EC,△BEG为等腰直角三角形,
∴∠AGE=180°-45°=135°,
又∵CF为正方形外角平分线,
∴∠ECF=90°+45°=135°,
∵∠AEF=90°,
∴∠GAE=90°-∠AEB=∠CEF,
在△AGE和△ECF中,
,
∴△AGE≌△ECF(ASA);
(2)四边形GEFD是平行四边形,
理由如下:过点F作FM⊥BH于M,过F作FN⊥DC于N,
易证△AGD≌△ABE,
∴GD=AE,∠BAE=∠ADG,
∵△AGE≌△ECF,
∴AE=EF,
∴GD=EF,
在△AGD和△EFM中,
,
∴△AGD≌△EFM(AAS),
∴GD=EF,
在△DFN和△BGE中,
,
∴△DFN≌△BGE(SAS),
∴DF=GE,
∴四边形GEFD是平行四边形.
∴AG=EC,△BEG为等腰直角三角形,
∴∠AGE=180°-45°=135°,
又∵CF为正方形外角平分线,
∴∠ECF=90°+45°=135°,
∵∠AEF=90°,
∴∠GAE=90°-∠AEB=∠CEF,
在△AGE和△ECF中,
|
∴△AGE≌△ECF(ASA);
(2)四边形GEFD是平行四边形,

理由如下:过点F作FM⊥BH于M,过F作FN⊥DC于N,
易证△AGD≌△ABE,
∴GD=AE,∠BAE=∠ADG,
∵△AGE≌△ECF,
∴AE=EF,
∴GD=EF,
在△AGD和△EFM中,
|
∴△AGD≌△EFM(AAS),
∴GD=EF,
在△DFN和△BGE中,
|
∴△DFN≌△BGE(SAS),
∴DF=GE,
∴四边形GEFD是平行四边形.
点评:此题主要考查了正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质等;综合性较强,难度适中.

练习册系列答案
相关题目
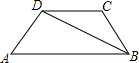 如图,在等腰梯形ABCD中,AB∥CD,AD=BC=4,∠A=60°,BD平分∠ABC,则这个梯形的面积是( )
如图,在等腰梯形ABCD中,AB∥CD,AD=BC=4,∠A=60°,BD平分∠ABC,则这个梯形的面积是( )A、6
| ||
B、8
| ||
C、10
| ||
D、12
|
 如图,正方形ABCD的边长为1,点F在线段CD上运动,AE平分∠BAF交BC边于点E.
如图,正方形ABCD的边长为1,点F在线段CD上运动,AE平分∠BAF交BC边于点E.